Giải bài 5 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo

Bài 5 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo:

Để làm một khung lồng đèn kéo quân hình lăng trụ lục giác ABCDEF.A'B'C'D'E'F', Bình gắn hai thanh tre A₁D₁, F₁C₁ song song với mặt phẳng đáy và cắt nhau tại O₁ (Hình 19)

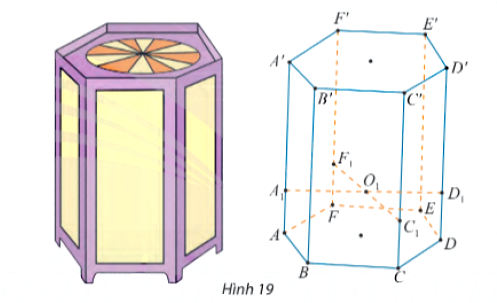
a) Xác định giao tuyến của mp(A₁D₁,F₁C₁) với các mặt bên của lăng trụ

b) Cho biết A′A₁=6AA₁ và AA' = 70 cm. Tính CC₁ và C₁C′

Phân tích và Hướng dẫn giải:

Đề bài cho một lồng đèn hình lăng trụ lục giác ABCDEF.A'B'C'D'E'F'. Hai thanh tre A₁D₁ và F₁C₁ song song với mặt đáy và cắt nhau tại O₁.

Bài toán có hai yêu cầu chính:

a) Xác định giao tuyến của mặt phẳng (A₁D₁, F₁C₁) với các mặt bên của lăng trụ: Giao tuyến của hai mặt phẳng song song với một mặt phẳng thứ ba cũng song song với các đường thẳng trong mặt phẳng đó.

b) Tính CC₁ và C₁C':Dựa vào tỉ lệ A'A₁ = 6AA₁ và AA' = 70 cm, ta sẽ tính được độ dài AA₁. Sau đó, sử dụng tính chất của hình lăng trụ và đường trung bình để tìm CC₁ và C₁C'.

Lời giải chi tiết:

a) Do mặt phẳng (A₁C₁D₁F₁) chứa hai đường thẳng cắt nhau A₁D₁ và C₁F₁ và cùng song song với mặt phẳng (ABCDEF)

Nên (A₁C₁D₁F₁)//(ABCDEF)

Gọi B1,E1 lần lượt là giao của mặt phẳng  (A₁C₁D₁F₁) với BB' và EE'

Ta có giao tuyến của (A₁C₁D₁F₁) với các mặt bên của lăng trụ là A₁B₁, B₁C₁, C₁D₁, D₁E₁, E₁F₁, F₁A₁

b) Ta có: A′A₁=6AA₁; AA′=70 nên AA₁=10

Do (ACC'A') cắt hai mặt phẳng (A₁C₁D₁F₁)//(ABCDEF) lần lượt tại A₁C₁ và AC nên A₁C₁//AC

Mà AA₁//CC₁ nên tứ giác AA₁C₁C là hình bình hành. 

Suy ra CC₁=AA₁=10

Mà CC' = AA' = 70

Nên C₁C′=70−10=60