Giải bài 7 trang 13 Toán 11 tập 1 SGK Chân trời sáng tạo
Chào các em! Hôm nay chúng ta sẽ cùng giải chi tiết Bài 7 trang 13 trong sách giáo khoa Toán 11 tập 1, bộ sách Chân trời sáng tạo. Bài tập này giúp các em làm quen với việc biểu diễn một họ các góc lượng giác trên đường tròn lượng giác. Để giải bài này, chúng ta sẽ xác định các điểm biểu diễn bằng cách thay thế các giá trị số nguyên cho k.
Đề Bài 7 trang 13 Toán 11 tập 1:
Trên đường tròn lượng giác hãy biểu diễn các góc lượng giác có số đo có dạng là:
a)
b)
Phân tích và Hướng dẫn giải
Để giải bài toán này, các em cần hiểu rõ ý nghĩa của công thức số đo tổng quát.
-
Công thức có dạng α0+kβ cho biết các điểm biểu diễn sẽ cách nhau một góc β trên đường tròn.
-
Việc của chúng ta là thay các giá trị nguyên của k (ví dụ: k=0,1,2,... và k=−1,−2,...) vào công thức để tìm các điểm biểu diễn.
-
Sau khi tìm được một số điểm, các em sẽ nhận ra quy luật và số lượng các điểm biểu diễn riêng biệt trên đường tròn.
Lời giải chi tiết:
a) Với k = 0 thì có góc lượng giác có số đo góc là , được biểu diễn bởi điểm M;
+ Với k = 1 thì có góc lượng giác có số đo góc là:
được biểu diễn bởi điểm N;
+ Với k = 2 thì có góc lượng giác có số đo góc là:
nên cũng được biểu diễn bởi điểm M;
+ Với k = 3 thì có góc lượng giác có số đo góc là:
nên cũng được biểu diễn bởi điểm N.
⇒ Với k chẵn thì các góc lượng giác có số đo dạng: được biểu diễn bởi điểm M;
Với k lẻ thì các góc lượng giác có số đo dạng: được biểu diễn bởi điểm N khi đó ta có hình vẽ sau:
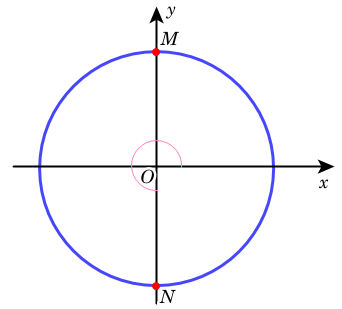
b) Với k = 0 thì có góc lượng giác có số đo góc là 0, được biểu diễn bởi điểm A;
+ Với k = 1 thì có góc lượng giác có số đo góc là được biểu diễn bởi điểm M;
+ Với k = 2 thì có góc lượng giác có số đo góc là được biểu diễn bởi điểm B;
+ Với k = 3 thì có góc lượng giác có số đo góc là được biểu diễn bởi điểm N;
+ Với k = 4 thì có góc lượng giác có số đo góc là được biểu diễn bởi điểm A’;
+ Với k = 5 thì có góc lượng giác có số đo góc là được biểu diễn bởi điểm M’;
Với k = 6 thì có góc lượng giác có số đo góc là được biểu diễn bởi điểm B’;
+ Với k = 7 thì có góc lượng giác có số đo góc là được biểu diễn bởi điểm N’;
+ Với k = 8 thì có góc lượng giác có số đo góc là nên được biểu diễn bởi điểm A;
⇒ Các góc lượng giác có số đo dạng: được biểu diễn bởi các điểm A, M, B, N, A’, M’, B’, N’. Khi đó ta có hình vẽ sau:
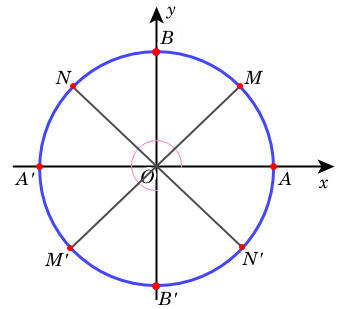
Qua bài tập này, các em đã học được cách xác định và biểu diễn một họ các góc lượng giác trên đường tròn lượng giác. Kỹ năng này không chỉ giúp các em hình dung trực quan hơn mà còn là nền tảng để giải các bài toán phức tạp hơn về hàm số lượng giác và phương trình lượng giác.
• Xem thêm:
Bài 1 trang 12 Toán 11 tập 1 SGK Chân trời sáng tạo: Đổi số đo của các góc dưới đây sang radian:...
Bài 2 trang 12 Toán 11 tập 1 SGK Chân trời sáng tạo: Đổi số đo của các góc sau đây sang độ:...
Đánh giá & nhận xét
-
 Giải bài 4 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 141 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 140 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 140 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 135 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 134 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 134 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo: Hình vuông nội tiếp đường tròn
Giải bài 3 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo: Hình vuông nội tiếp đường tròn
-
 Giải bài 2 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 126 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 120 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 119 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 119 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 112 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 111 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 111 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 106 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 105 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 105 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 99 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 85 Toán 11 tập 1 SGK Chân trời sáng tạo


















































