Giải bài 14 trang 106 SGK Toán 9 tập 1

Bài 14 trang 106 SGK Toán 9 tập 1:

Cho đường tròn tâm O bán kính 25cm, dây AB bằng 40cm. Vẽ dây CD song song với AB và có khoảng cách đến AB bằng 22cm. Tính độ dài dây CD.

Giải bài 14 trang 106 SGK Toán 9 tập 1:

Ta có hình minh hoạ như sau: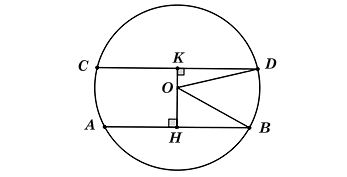

Vẽ OH ⊥ AB tại H, đường thẳng OH cắt CD tại K

Vì AB // CD mà OH ⊥ AB nên OH ⊥ CD hay OK ⊥ CD

Ta có: OK ⊥ CD và OH ⊥ AB

 (do đường kính vuông góc với dây thì đi qua trung điểm của dây ấy)

Ta có: OB = OD = R = 25cm

• Xét ΔOBH vuông tại H (do OH ⊥ AB)

Áp dụng định lí Py-ta-go ta có:

OB² = OH² + HB²

⇒ OH² = OB² – BH²

⇒ OH² = 25² – 20² = 225

⇒ OH =  = 15 (cm)

Lại có: HK = OH + OK

⇒ OK = HK – OH = 22 – 15 = 7 (cm) (HK là khoảng cách giữa hai dây song song AB và CD).

• Xét ΔOKD vuông tại K (do OK ⊥ CD)

Áp dụng định lí Py-ta-go ta có:

OD² = OK² + KD²

⇒ KD² = OD² – OK² = 25² – 7² = 576

⇒ KD =  = 24 (cm)

⇒ CD = 2KD = 2.24 = 48 (cm).