Giải bài 11 trang 104 SGK Toán 9 tập 1: Đường tròn và hình thang

Đề bài:

Cho đường tròn (O) đường kính AB, dây CD không cắt đường kính AB, Gọi H và K theo thứ tự là chân các đường vuông góc kẻ từ A và B đến CD. Chứng minh rằng CH = DK.

Phân tích và Hướng dẫn giải

Để chứng minh $CH=DK$, ta cần sử dụng các tính chất sau:

1. Đường trung bình của hình thang: Nếu một đường thẳng đi qua trung điểm một cạnh bên của hình thang và song song với hai đáy thì nó đi qua trung điểm cạnh bên thứ hai.

2. Đường kính vuông góc với dây: Trong một đường tròn, đường kính vuông góc với một dây thì đi qua trung điểm của dây đó.

Ta sẽ thực hiện các bước sau:

• Kẻ đường phụ để tạo ra một hình thang.

• Sử dụng tính chất đường kính vuông góc với dây để tìm một mối quan hệ về trung điểm.

• Kết hợp các mối quan hệ trên để suy ra điều cần chứng minh.

Lời giải chi tiết bài 11 trang 104 Toán 9:

Ta có hình vẽ minh hoạ như sau:

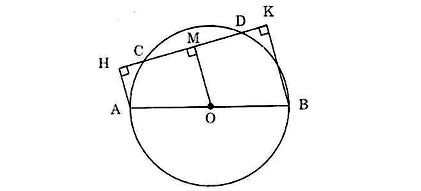
Kẻ OM ⊥ CD.

Vì AH // BK (cùng vuông góc HK) nên tứ giác AHKB là hình thang.

• Xét hình thang AHKB có:

 AO = OB (bán kính).

 OM // AH // BK (cùng vuông góc HK)

⇒ OM là đường trung bình của hình thang.

=> MH = MK  (*)

Vì OM ⊥ CD nên MC = MD   (**)

Từ (*) và (**) suy ra CH = DK. (đpcm)