Cách chứng minh các điểm (4 điểm) cùng thuộc một đường tròn - Toán 9 chuyên đề

Phương pháp chứng minh 4 điểm thuộc một đường tròn

Có hai phương pháp chính để chứng minh nhiều điểm cùng thuộc một đường tròn:

1. Sử dụng định nghĩa: Chứng minh rằng các điểm đó cùng cách đều một điểm $O$ cố định. Điểm $O$ này chính là tâm của đường tròn.

2. Sử dụng tính chất của tứ giác nội tiếp: Chứng minh rằng một tứ giác có các đỉnh là 4 điểm cần chứng minh là một tứ giác nội tiếp. Một số dấu hiệu nhận biết tứ giác nội tiếp phổ biến là:

   • Tứ giác có tổng hai góc đối bằng 180^o.

   • Tứ giác có hai đỉnh kề nhau cùng nhìn một cạnh dưới một góc bằng nhau.

   • Tứ giác có bốn đỉnh cùng cách đều một điểm.

Mở rộng: Chẳng hạn để chứng minh 5 điểm A, B, C, D, E cùng thuộc một đường tròn ta chứng minh 4 điểm ABCD và 4 điểm ABCE là các tứ giác nội tiếp cùng một đường tròn tâm O.

Dưới đây là một số ví dụ minh họa chi tiết.

Ví dụ 1: Cho tam giác ABC vuông tại A, đường cao AH. Từ M là điểm bất kì trên cạnh BC kẻ MD ⊥ AB, ME ⊥ AC. Chứng minh 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.

Lời giải:

- Theo bài ra, có có hình sau: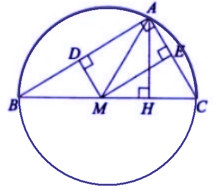

Xét tam giác vuông ADM có cạnh huyền AM

Xét tam giác vuông AEM có cạnh huyền AM

Và tam giác vuông AHM có cạnh huyền AM

Các tam giác này đều có chung cạnh huyền AM nên 3 đỉnh góc vuông nằm trên đường tròn đường kính AM có tâm là trung điểm của AM.

Vậy 5 điểm A, D, M, H, E cùng nằm trên một đường tròn.

Ví dụ 2: Cho tam giác ABC vuông tại A gọi D là điểm đối xứng với A qua cạnh BC. Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn.

Lời giải:

- Ta có hình vẽ như sau:

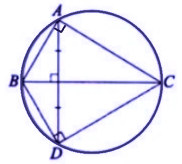
Vì D đối xứng với  A qua BC, B đối xứng với B qua BC, C đối xứng với C qua BC nên 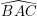 đối xứng với góc  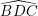qua BC.

Suy ra ∠BDC = ∠BAC = 90⁰

Xét tam giác vuông BAC và BDC có chung cạnh huyền BC nên hai đỉnh góc vuông A, D nằm trên đường tròn đường kính BC, có tâm là trung điểm của cạnh huyền BC.

Vậy 4 điểm A, B, C, D cùng nằm trên một đường tròn.

Ví dụ 3: Cho tam giác ABC vuông tại A. Trên AC lấy điểm D. Hình chiếu của D lên BC là E, điểm đối xứng của E qua BD là F. Chứng minh 5 điểm A, B, E, D, F cùng nằm trên một đường tròn. Xác định tâm O của đường tròn đó.

Lời giải:

- Ta có hình vẽ như sau:

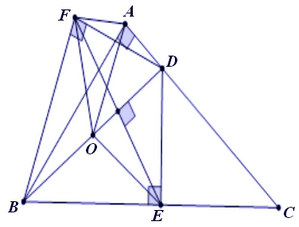- Theo giả thuyết, DE ⊥ BC nên ∠BEB = 90⁰

- Vì E và F đối xứng với nhau qua BD nên BD là đường trung trực của đoạn thẳng EF nên suy ra:

 BF = BE và DF = DE

Suy ra: ΔBFD = ΔBED (c-c-c)

Suy ra: ∠BFD = ∠BEB = 90⁰

- Gọi O là trung điểm của BD.

- Xét tam giác vuông ABD vuông tại A có AO là trung tuyến nên:

 AO = ½BD = OB = OD   (1)

- Xét tam giác vuông BDE vuông tại E có OE là trung tuyến nên:

 EO = ½BD = OB = OD   (2)

- Xét tam giác vuông BFD vuông tại F có OF là trung tuyến nên:

 FO = ½BD = OB = OD   (3)

Từ (1), (2) và (3) suy ra: OA = OB = OD = OE = OF.

Vậy 5 điểm A, B, E, D, F cùng nằm trên một đường tròn tâm O với O là trung điểm của BC.

Ví dụ 4: Cho hình thang cân ABCD (với AD//BC) có AB = 12cm, AC = 16cm, BC = 20 cm. Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.

Lời giải:

- Ta có hình minh họa như sau:

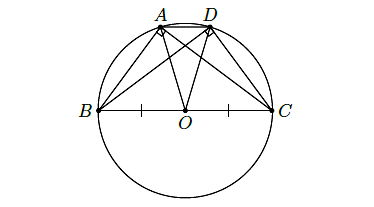Vì ABCD là hình thang cân với 2 đáy AD, BC nên AB = CD = 12 cm và BD = AC = 16 cm

Gọi O là trung điểm của BC,

Xét ΔABC có:

AB² + AC² = 12² + 16² = 20² = BC²

Vậy ΔABC vuông tại A. Vì vậy 3 đỉnh của tam giác ABC cùng thuộc đường tròn tâm O.

Tượng tự, ta cũng có ΔBCD vuông tại D. Vì vậy 3 đỉnh của tam giác BCD cùng thuộc đường tròn tâm O.

Vậy 4 điểm A, B, C, D cùng thuộc đường tròn (O) bán kính R = BC/2 = 20/2 = 10 (cm).

Ví dụ 5: Cho tứ giác ABCD có 

a) Chứng minh 4 điểm A, B, C, D cùng thuộc một đường tròn

b) Nếu AC = BD thì tứ giác ABCD là hình gì?

Lời giải:

Ta có hình minh họa như sau:

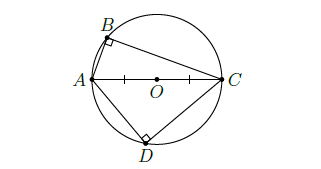
a) Gọi O là trung điểm của AC

Vì tam giác ABC vuông tại B nên ba đỉnh A, B, C cùng thuộc đường tròn (O)

Vì tam giác ACD vuông tại D nên ba đỉnh A, C, D cùng thuộc đường tròn (O)

Vậy 4 điểm A, B, C, D cùng thuộc đường tròn (O) đường kính AC

b) Nếu BD = AC thì BD là đường kính của (O)

Suy ra 

Vậy tứ giác ABCD có  

Nên ABCD là hình chữ nhật.