Bài 7.34 trang 43 Toán 7 Tập 2 Kết nối tri thức

Bài 7.34 Trang 43 Toán 7 Kết nối tri thức Tập 2: 

Trong mỗi trường hợp sau đây, tìm thương Q(x) và dư R(x) trong phép chia F(x) cho G(x) rồi biểu diễn F(x) dưới dạng: F(x) = G(x) . Q(x) + R(x).

a) F(x) = 6x⁴ - 3x³ + 15x² + 2x - 1; G(x) = 3x².

b) F(x) = 12x⁴ + 10x³ - x - 3; G(x) = 3x² + x + 1.

Nguyên tắc Phép chia đa thức

Phép chia kết thúc khi bậc của đa thức dư $R(x)$ nhỏ hơn bậc của đa thức chia $G(x)$.

Giải Bài 7.34 Trang 43 Toán 7 Kết nối tri thức Tập 2: 

a) Thực hiện đặt phép chia ta được:

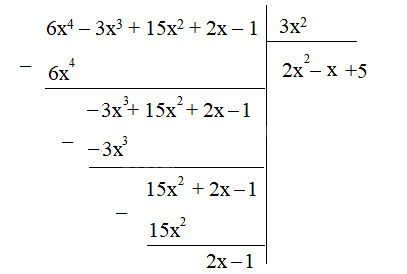
Thương là: Q(x) = 2x² - x + 5;

Dư là: R(x) = 2x - 1.

Vậy có: F(x) = 6x⁴ - 3x³ + 15x² + 2x - 1 = 3x² . (2x² - x + 5) + 2x - 1.

b) Thực hiện phép chia ta được:

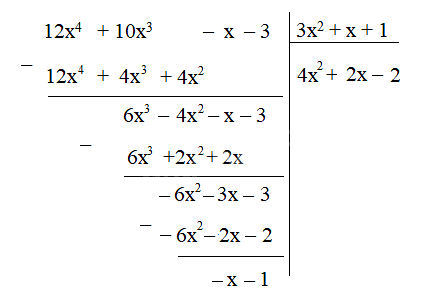
Thương là: Q(x) = 4x² + 2x - 2;

Dư là: R(x) = -x - 1.

Vậy có: F(x) = 12x⁴ + 10x³ - x - 3 = (3x² + x + 1) . (4x² + 2x - 2) - x - 1.