Bài 7.32 trang 43 Toán 7 Tập 2 Kết nối tri thức
Bài tập 7.32, trang 43 SGK Toán 7 Tập 2 (Kết nối tri thức), yêu cầu học sinh thực hiện phép chia đa thức cho đa thức bằng phương pháp đặt tính chia (chia cột). Đây là phương pháp nền tảng giúp xác định thương và số dư của phép chia khi cả số chia và số bị chia đều là đa thức.
Bài 7.32 Trang 43 Toán 7 Kết nối tri thức Tập 2:
Thực hiện các phép chia đa thức sau bằng cách đặt tính chia:
a) (6x3 - 2x2 - 9x + 3) : (3x - 1);
b) (4x4 + 14x3 - 21x - 9) : (2x2 - 3).
Quy tắc Đặt tính chia đa thức
-
Sắp xếp đa thức bị chia và đa thức chia theo lũy thừa giảm dần của biến.
-
Chia hạng tử bậc cao nhất của đa thức bị chia cho hạng tử bậc cao nhất của đa thức chia để được hạng tử đầu tiên của thương.
-
Nhân hạng tử này với đa thức chia và trừ đi đa thức bị chia để được đa thức dư thứ nhất.
-
Tiếp tục chia đa thức dư thứ nhất cho đa thức chia, lặp lại cho đến khi bậc của đa thức dư nhỏ hơn bậc của đa thức chia (hoặc bằng $0$).
Giải Bài 7.32 Trang 43 Toán 7 Kết nối tri thức Tập 2:
a) Thực hiện đặt phép chia ta được:
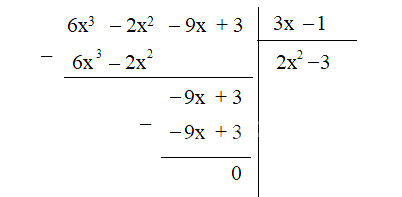
Giải thích:
-
Lượt 1: $6x^3 : 3x = 2x^2$. Nhân $2x^2(3x - 1) = 6x^3 - 2x^2$. Trừ, ta được $0$. Hạ $-9x + 3$.
-
Lượt 2: $-9x : 3x = -3$. Nhân $-3(3x - 1) = -9x + 3$. Trừ, ta được $0$.
b) Thực hiện đặt phép chia ta được:
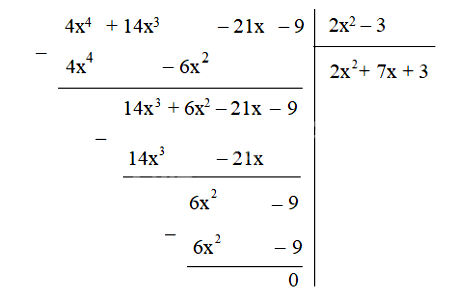
Giải thích:
-
Lượt 1: $4x^4 : 2x^2 = 2x^2$. Nhân $2x^2(2x^2 - 3) = 4x^4 - 6x^2$. Trừ, ta được $14x^3 + 6x^2$. Hạ $-21x - 9$.
-
Lượt 2: $14x^3 : 2x^2 = 7x$. Nhân $7x(2x^2 - 3) = 14x^3 - 21x$. Trừ, ta được $6x^2 - 9$.
-
Lượt 3: $6x^2 : 2x^2 = 3$. Nhân $3(2x^2 - 3) = 6x^2 - 9$. Trừ, ta được $0$.
Như vậy, ta có kết quả như sau:
| Phần | Phép chia | Thương | Số dư |
| a | $(6x^3 - 2x^2 - 9x + 3) : (3x - 1)$ | $\mathbf{2x^2 - 3}$ | $0$ |
| b | $(4x^4 + 14x^3 - 21x - 9) : (2x^2 - 3)$ | $\mathbf{2x^2 + 7x + 3}$ | $0$ |
• Xem thêm:
Bài 7.30 Trang 43 Toán 7 Kết nối tri thức Tập 2: Tính: a) 8x5 : 4x3; b) 120x7 : (-24x5);...
Đánh giá & nhận xét
-
 Bài 9.9 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.9 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.8 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.8 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.7 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.7 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.6 trang 65 Toán 7 Tập 2 Kết nối tri thức
Bài 9.6 trang 65 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.35 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.35 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.34 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.34 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.33 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.33 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.32 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.32 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.31 trang 83 Toán 7 Tập 2 Kết nối tri thức
Bài 9.31 trang 83 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.30 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.30 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.29 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.29 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.28 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.28 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.27 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.27 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.26 trang 81 Toán 7 Tập 2 Kết nối tri thức
Bài 9.26 trang 81 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.25 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.25 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.24 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.24 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.23 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.23 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.22 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.22 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.21 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.21 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.20 trang 76 Toán 7 Tập 2 Kết nối tri thức
Bài 9.20 trang 76 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.19 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.19 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.18 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.18 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.17 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.17 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.16 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.16 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.15 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.15 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.14 trang 71 Toán 7 Tập 2 Kết nối tri thức
Bài 9.14 trang 71 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.13 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.13 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.12 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.12 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.11 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.11 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 9.10 trang 69 Toán 7 Tập 2 Kết nối tri thức
Bài 9.10 trang 69 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.7 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.7 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.6 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.6 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.5 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.5 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.4 trang 55 Toán 7 Tập 2 Kết nối tri thức
Bài 8.4 trang 55 Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.15 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.15 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.14 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.14 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.13 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.13 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.12 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.12 SGK Toán 7 Tập 2 Kết nối tri thức
-
 Bài 8.11 SGK Toán 7 Tập 2 Kết nối tri thức
Bài 8.11 SGK Toán 7 Tập 2 Kết nối tri thức


















































