Bài 2.8 trang 58 Toán 12 tập 1 Kết nối tri thức

Đề bài:

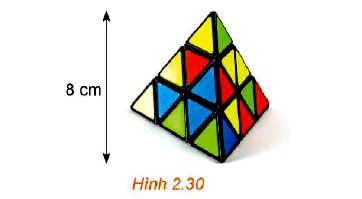
Trong Luyện tập 8, ta đã biết trọng tâm của tứ diện ABCD là một điểm I thỏa mãn   ở đó G là trọng tâm của tam giác BCD. Áp dụng tính chất trên để tính khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó, biết rằng chiều cao của khối rubik là 8cm (H.2.30).

Phân tích và Hướng dẫn giải:

Để giải bài toán này, các em cần nhớ lại định nghĩa về trọng tâm của tứ diện.

Trọng tâm của tứ diện là giao điểm của các đoạn thẳng nối một đỉnh với trọng tâm của mặt đối diện.

Trong một tứ diện ABCD nếu I là trọng tâm, G là trọng tâm tam giác BCD, thì I nằm trên đoạn AG và thỏa mãn: $\vec{IA} + \vec{IB} + \vec{IC} + \vec{ID} = \vec{0}$. Một tính chất đặc biệt của trọng tâm tứ diện là nó chia đoạn thẳng nối đỉnh với trọng tâm mặt đối diện thành tỉ lệ 3:1. Cụ thể, $\vec{AI} = \frac{3}{4}\vec{AG}$.

Trong bài toán này, khối rubik là một tứ diện đều, nên các tính chất trên vẫn đúng. Khoảng cách từ trọng tâm của tứ diện đến một mặt chính là 1/4 chiều cao của tứ diện.

Lời giải chi tiết:

Ta có hình minh họa như sau:

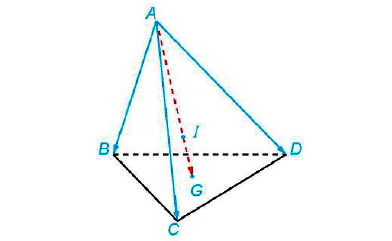Đặt tên khối rubik là tứ diện đều ABCD có G là trọng tâm tam giác BCD, I là trọng tâm tứ diện ABCD.

Vì vậy, 

Vì chiều cao của rubik bằng 8cm nên: AG = 8 cm 

Nên 

Vậy khoảng cách từ trọng tâm của một khối rubik (đồng chất) hình tứ diện đều đến một mặt của nó bằng 2cm.