Bài 2.7 trang 58 Toán 12 tập 1 Kết nối tri thức

Đề bài:

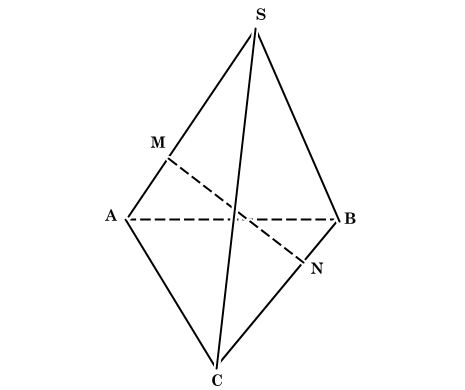
Cho hình chóp S.ABC. Trên cạnh SA, lấy điểm M sao cho SM = 2AM. Trên cạnh BC, lấy điểm N sao cho CN = 2BN. Chứng minh rằng: 

Phân tích và Hướng dẫn giải

Để chứng minh đẳng thức vectơ, chúng ta thường sử dụng quy tắc ba điểm (quy tắc xen điểm) để phân tích các vectơ đã cho. Mục tiêu là biến đổi vế trái của đẳng thức sao cho nó bằng vế phải.

Cụ thể, để biểu diễn vectơ  theo các vectơ  và , chúng ta có thể chèn một điểm thích hợp vào giữa. Trong trường hợp này, việc chèn điểm A và điểm B là một lựa chọn hợp lý.

Ta sẽ thực hiện các bước sau:

1. Phân tích vectơ : Sử dụng quy tắc ba điểm để phân tích  thành tổng của các vectơ đi qua các đỉnh của hình chóp (A, B).

2. Biểu diễn các vectơ mới: Dựa vào các dữ kiện về vị trí của các điểm M, N để biểu diễn các vectơ  và  theo các vectơ  và .

3. Thay thế và rút gọn: Thay các biểu thức đã tìm được vào đẳng thức ban đầu để hoàn tất chứng minh.

Lời giải chi tiết:

Ta có hình minh họa như sau:

Ta có:

 (đpcm)