Toán 12 - Ứng dụng đạo hàm, khảo sát hàm số và vẽ đồ thị
Khảo sát hàm số gồm mấy bước? Làm sao để khảo sát một hàm số cho trước như hàm số bậc 3, hàm trùng phương, hay hàm số hữu tỉ.
Sau khi đọc xong bài viết này, bạn chắc chắn sẽ hiểu rõ làm thế nào để có thể khảo sát hàm số bậc 3, hàm bậc 4 (trùng phương), hàm hữu tỉ hay một hàm số bất kỳ.
I. Một số kiến thức cần nhớ về Hàm số
1. Sự đồng biến, nghịch biến của hàm số.
_ Hàm f(x) đồng biến trên (a,b) ⇔ f'(x) ≥ 0 ∀ x ∈ (a,b)
_ Hàm f(x) nghịch biến trên (a,b) ⇔ f'(x) ≤ 0 ∀ x ∈ (a,b)
2. Cực đại và cực tiểu của hàm số.
* Qui tắc 1:
+ Tìm tập xác định D.
+ Tính f’(x). Tìm các điểm xi Î D (i =1,2,…) tại đó đạo hàm f’(x) = 0 hoặc f’(x) không xác định .
+ Lập bảng xét dấu của f’(x)
+ Kết luận: Nếu f’(x) đổi dấu từ (+) sang (-) khi x qua x0 thì x0 là điểm cực đại và ngược lại thì x0 là điểm cực tiểu của hàm số
* Qui tắc 2:
+ Tìm tập xác định D.
+ Tìm f’(x). Giải phương trình f’(x)=0, tìm các nghiệm xi (i =1,2,…).
+ Tim f’’(x) và tính f’’(xi).
+ Kết luận:
- Nếu f’’(xi) < 0 thì xi là điểm cực đại
- Nếu f’’(xi) > 0 thì xi là điểm cực tiểu.
3. Giá trị lớn nhất và giá trị nhỏ nhất.
a) Tìm GTLN và GTNN trên [a,b]:
+ Bước 1: Tìm các điểm x1,x2,…xn tại đó f’(x) = 0 hoặc f’(x) không xác định trên [a,b].
+ Bước 2: Tính f(a), f(x1),f(x2),…f(xn), f(b).
+ Bước 3: GTLN là số lớn nhất M và GTNN là số nhỏ nhất m trong các số trên.
b) Tìm GTLN và GTNN trên (a; b), [a; b), (a; b]: Ta cần lập bảng biến thiên
4. Tiệm cận của đồ thị hàm số:
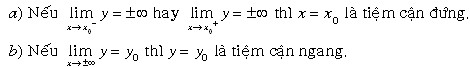
5. Khảo sát hàm số và các bài toán liên quan.
* Các bước khảo sát hàm số:
- Bước 1: Tìm tập xác định D
- Bước 2: Sự biến thiên.
+ Tính y’. y'=0; xét dấu y’ tìm khoảng tăng, giảm.
+ Kết luận cực trị.
+ Tính giới hạn, tiệm cận (nếu có).
+ Lập bảng biến thiên
- Bước 3: Tìm 1 vài điểm của hàm số và vẽ đồ thị
II. Áp dụng khảo sát hàm số vô tỉ, hữu tỉ
* Áp dụng khảo sát và vẽ đồ thị hàm số bậc 3: y=x3+3x2−4
Bước 1: Tập xác định: D = R
Bước 2: Sự biến thiên
- Có: y′=3x2+6x; cho y’ = 0 <=> y′=3x2+6x = 0 <=> x=0 hoặc x=−2
Hàm số nghịch biến trong khoảng (-2; 0)
Hàm số đồng biến trong khoảng (-∞; -2) và (0; +∞)
– Cực trị:
Hàm số đạt cực đại tại x = -2; yCD = y(-2) = 0
Hàm số đạt cực tiểu tại x = 0; yCT=y(0) = -4
- Giới hạn của hàm số tại vô cực:
![]()
– Lập bảng biến thiên
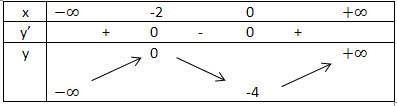
Bước 3: Tìm 1 số điểm để vẽ đồ thị
- Giao của đồ thị với trục Ox: y=0 <=> x3+3x2-4=0 <=> (x-1)(x+2)2=0 <=> x=1 hoặc x=-2
* Lưu ý: hàm số bậc 3 trong các bài toán khảo sát thường có nghiệm đặc biệt x=1,-1,0,... sau đó chia đa thức để đưa về dạng tích các đa thức như trên.
Vậy (1,0) và (-2,0) là giao điểm của đồ thị với trục Ox
- Giao của đồ thị với trục Oy: x=0 <=> y=-4. Vậy (0,-4) là giao của đồ thị với Oy
Ta có bảng giá trị:
| x | -2 | -1 | 0 | 1 |
| y | 0 | -2 | -4 | 0 |
- Tìm điểm uốn y''=6x+6=0 <=> x=-1 thay vào hàm số được y=-2;
Vậy điểm uốn là U(-1,-2)
Đồ thị (C)
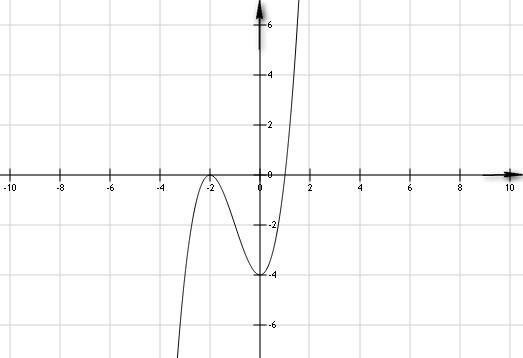
- Áp dụng khảo sát và vẽ đồ thị hàm số bậc 4: y=x4-2x2−3
Bước 1: Tập xác định D = R
Bước 2: Sự biến thiên
y’ = 4x3 - 4x
y’ = 0 <=> 4x3 - 4x = 0 <=> x(4x2 – 4) = 0 <=> x = 0 hoặc x = 1 hoặc x = - 1
Hàm số nghịch biến trong khoảng (-∞; -1) và (0; 1)
Hàm số đồng biến trong khoảng (-1; 0) và (1; +∞)
– Cực trị:
Hàm số đạt cực đại tại x = 0; yCD = y(0) = -3
Hàm số đạt cực tiểu tại x = -1; yCT=y(-1) = -4
Giới hạn:
![]()
Lập bảng biến thiên:
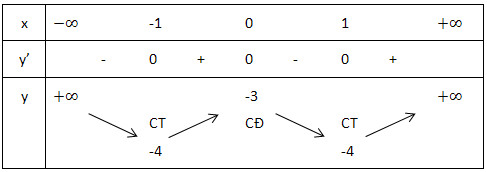
Bước 3: Tìm 1 số điểm để vẽ đồ thị
Đồ thị hàm số:
Giao điểm với Ox:x = √3; y = 0; x = -√3; y = 0
Giao điểm với Oy: x = 0 ; y = - 3
Bảng giá trị:
| x | -√3 | 0 | √3 |
| y | 0 | -3 | 0 |
- Tìm điểm uốn y''=12x2 - 4=0 <=> x=-1/√3 hoặc x = 1/√3;
Vậy điểm uốn là U1(-1/√3,-32/9) và U1(1/√3,-32/9)
Đồ thị:
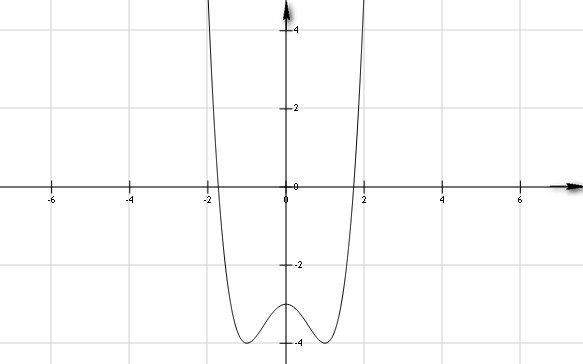
- Áp dụng khảo sát hàm hữu tỉ bậc nhất: y=(ax+b)/(cd+d)
Khảo sát sự biến thiên và vẽ đồ thị của hàm số: y = (2x - 1)(x - 1)
Bước 1: Hàm số có tập xác định là R∖{1}
Bước 2: Sự biến thiên của hàm số
y’ = -1/(x-1)2 <0 với mọi x ≠1
Hàm số nghịch biến trong khoảng (-2;-∞) và (+∞; 2)
Giới hạn: giới hạn vô cực và các tiệm cận ta có
![]()
=> x=1 là tiệm cận đứng
![]()
=> y=2 là tiệm cận ngang
Lập bảng biến thiên:
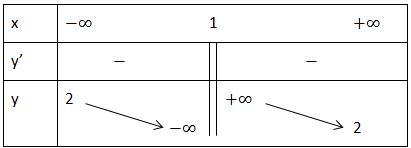
Bước 3: Tìm 1 số điểm để vẽ đồ thì hàm số
Giao Ox: y=0 thì x = -1/2
Giao Oy: x=0 thì y = 2
Đồ thị:
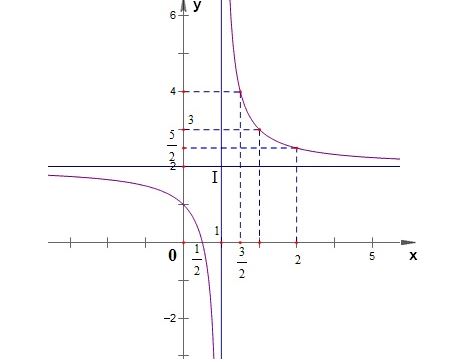
- Áp dụng khảo sát hàm hữu tỉ bậc 2 trên bậc 1: y=(ax2 + bx + c)/(a'x + b') (với a, a' khác 0)
Khảo sát sự biến thiên và vẽ đồ thị của hàm số: y=(x2 − 2x − 3)/(x−2)
Có thể viết hàm số đã cho dưới dạng: y= x - 3/(x-2)
Bước 1: Tập xác định của hàm số: x ≠ 2 hay R∖{2}
Bước 2: Sự biến thiên của hàm số
y’ = 1+ 3/(x-2)2 >0 với mọi x ≠2
Hàm số đồng biến trong khoảng (-∞; 2) và (2 ;+∞)
Giới hạn: giới hạn vô cực và các tiệm cận ta có
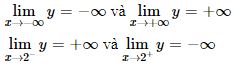
=> x=2 là tiệm cận đứng
![]()
=> y=x là tiệm cận xiên
Lập bảng biến thiên:
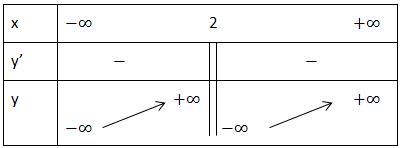
Bước 3: Tìm 1 số điểm để vẽ đồ thị
Giao Ox: y=1 thì x = -1 hoặc x = 3
Giao Oy: x=0 thì y = 3/2
Đồ thị:
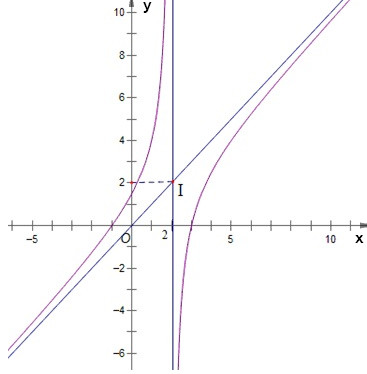
|
>> có thể bạn muốn xem: |
Hy vọng với phần ôn tập chi tiết về Ứng dụng Đạo hàm để khảo sát hàm số ở trên các em đã hiểu rõ để vận dụng vào bài tập. Các em có thể Đăng nhập vào trang Hay học hỏi (nếu chưa có tài khoản hãy Đăng Ký) để làm kiểm tra trắc nghiệm thử về các vấn đề liên quan tới hàm số TẠI ĐÂY.
Đánh giá & nhận xét





-
 Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 7 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 6 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
Bài 5 trang 12 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 4 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 3 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 2 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
Bài 1 trang 11 Toán 12 tập 2 Chân trời sáng tạo
-
 Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.18 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.17 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.16 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.15 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.14 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.13 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.12 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.11 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.10 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.9 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.8 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.7 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.6 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.5 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.4 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.3 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.2 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
Bài 4.1 SGK Toán 12 tập 2 Kết nối tri thức
-
 Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
Bài 15 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
Bài 14 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
Bài 13 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
Bài 12 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
Bài 11 trang 83 Toán 12 tập 1 Cánh Diều
-
 Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
Bài 10 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
Bài 9 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
Bài 8 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
Bài 7 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
Bài 6 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
Bài 5 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
Bài 4 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
Bài 3 trang 82 Toán 12 tập 1 Cánh Diều
-
 Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ
Bài 2 trang 82 Toán 12 tập 1 Cánh Diều: Tọa Độ Vectơ


















































