Giải bài 3 trang 100 SGK Toán 9 tập 1: Tam giác vuông,đường tròn ngoại tiếp

Đề bài:

Chứng minh các định lí sau:

a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền

b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp thì tam giác đó là tam giác vuông.

Phân tích và Hướng dẫn giải

Bài toán này bao gồm hai phần, mỗi phần là một định lí đảo của nhau. Để chứng minh, ta cần sử dụng các kiến thức sau:

• Tính chất đường trung tuyến trong tam giác vuông: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền.

• Định lí đảo về đường trung tuyến: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó, thì tam giác đó là tam giác vuông.

• Định nghĩa đường tròn ngoại tiếp: Đường tròn ngoại tiếp tam giác là đường tròn đi qua ba đỉnh của tam giác. Tâm của đường tròn này cách đều ba đỉnh.

Lời giải chi tiết bài 3 trang 100 Toán 9:

Ta có hình minh họa như sau:

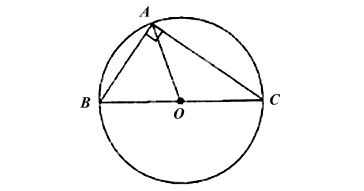
a) Xét tam giác ABC vuông tại A.

Gọi O là trung điểm của BC.

Ta có AO là đường trung tuyến ứng với cạnh huyền nên OA = OB = OC.

⇒ O là tâm của đường tròn đi qua A, B, C.

Vậy tâm của đường tròn ngoại tiếp ΔABC là trung điểm của cạnh huyền BC. (đpcm)

b) Xét tam giác ABC nội tiếp đường tròn (O) đường kính BC, ta có:

 OA = OB = OC

Tam giác ABC có đường trung tuyến AO bằng nửa cạnh BC

Suy ra tam giác ABC vuông tại A. (đpcm)