Bài 1.14 SGK Toán 12 tập 1 Kết nối tri thức

Bài 1.14 trang 19 Toán 12 Tập 1 Kết nối tri thức:

Một nhà sản xuất muốn thiết kế một chiếc hộp có dạng hình hộp chữ nhật không có nắp, có đáy là hình vuông và diện tích bề mặt bằng 108 cm² như Hình 1.17. Tìm các kích thước của chiếc hộp sao cho thể tích của hộp là lớn nhất.

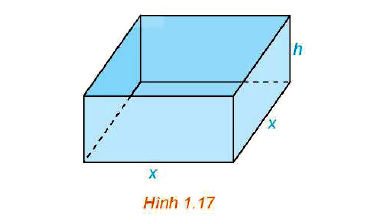
Giải bài 1.14 trang 19 Toán 12 Tập 1 Kết nối tri thức:

Hình hộp trên có độ dài cạnh đáy là x (cm) (x > 0) và chièu cao là h (cm) (h > 0)

Diện tích bề mặt của hình hộp là 108 cm² nên: x² + 4xh = 108

Thể tích của hình hộp là: 

Ta có: 

Bảng biến thiên:

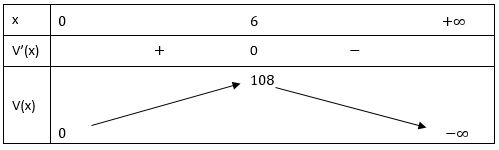
Nên thể tích của hình hộp là lớn nhất khi độ dài cạnh đáy x = 6 cm.

Khi đó, chiều cao của hình hộp là: