Giải 1.13 Toán 12 tập 1 SGK Kết nối tri thức

Đề bài:

Trong các cạnh của hình chữ nhật có chu vi là 24 cm, hãy tìm hình chữ nhật có diện tích lớn nhất.

Phân tích và Hướng dẫn giải

Để giải bài toán này, chúng ta sẽ sử dụng phương pháp sau:

1. Thiết lập hàm số:

   • Gọi các kích thước của hình chữ nhật là $x$ và $y$.

   • Dựa vào dữ kiện chu vi, biểu diễn một kích thước theo kích thước còn lại.

   • Lập hàm số biểu thị diện tích $S$ của hình chữ nhật theo một biến.

2. Tìm giá trị lớn nhất:

   • Tìm tập xác định của hàm số diện tích.

   • Sử dụng đạo hàm để tìm giá trị lớn nhất của hàm số.

   • Lập bảng biến thiên để xác định điểm cực đại, đó chính là điểm mà tại đó diện tích đạt giá trị lớn nhất.

Lời giải chi tiết:

Gọi x (cm) chiều dài của hình chữ nhật là x (0 < x < 12)

Chiều rộng của hình chữ nhật là: 12 - x (cm)

Diện tích của hình chữ nhật là: x(12 - x) = -x² + 12x (cm²)

Đặt S(x) = -x² + 12x, với x ∈ (0; 12)

S'(x) = -2x + 12 = 0 ⇔ x = 6 (thỏa)

Bảng biến thiên:

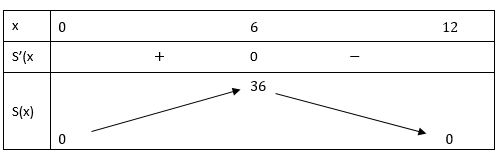
Vậy, trong các hình có cùng chu vi thì hình chữ nhật có diện tích lớn nhất là 36 cm².