Bài 7.40 trang 56 Toán 8 Tập 2 Kết nối tri thức

Bài 7.40 trang 56 Toán 8 Tập 2 Kết nối tri thức:

Trong lí thuyết tài chính, giá trị sổ sách là giá trị của một tài sản mà công ty sử dụng để xây dựng bảng cân đối kế toán của mình. Một số công ty khấu hao tài sản của họ bằng cách sử dụng phương pháp khấu hao đường thẳng để giá trị của tài sản giảm một lượng cố định mỗi năm. Mức suy giảm phụ thuộc vào thời gian sử dụng hữu ích mà công ty đặt tài sản đó. Giả sử một công ty vừa mua một chiếc máy photocopy mới với giá 18 triệu đồng. Công ty lựa chọn cách tính khấu hao chiếc máy photocopy này theo phương pháp khấu hao đường thẳng trong thời gian 3 năm, tức là mỗi năm giá trị của chiếc máy photocopy sẽ giảm 18 : 3 = 6 triệu đồng.

a) Viết hàm số bậc nhất biểu thị giá trị sổ sách V(x) của máy photocopy dưới dạng một hàm số theo thời gian sử dụng x (năm) của nó.

b) Vẽ đồ thị của hàm số bậc nhất y = V(x).

c) Giá trị sổ sách của máy photocopy sau 2 năm sử dụng là bao nhiêu?

d) Sau thời gian sử dụng là bao lâu thì máy photocopy có giá trị sổ sách là 9 triệu đồng?

Phân tích Khấu hao Đường thẳng

Giá trị sổ sách $V(x)$ sau $x$ năm được tính bằng công thức:

Trong đó $0 \le x \le 3$ (năm).

Giải Bài 7.40 trang 56 Toán 8 Tập 2 Kết nối tri thức:

a) Vì mỗi năm giá trị của chiếc máy photocopy sẽ giảm 6 triệu đồng nên x năm thì giá trị của chiếc máy này sẽ giảm 6x triệu đồng.

Do đó, hàm số bậc nhất biểu thị giá trị sổ sách của máy photocopy là V(x) = 18 – 6x.

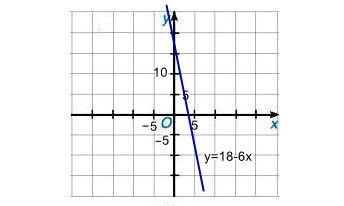
b) Vẽ đồ thị hàm số y = V(x) = 18 – 6x.

Cho x = 0 thì y = 18, ta được giao điểm của đồ thị với trục Oy là A(0; 18).

Cho y = 0 thì x = 3, ta được giao điểm của đồ thị với trục Oy là B(3; 0).

Đồ thị hàm số y = 18 – 6x là đường thẳng AB.

c) Giá trị sổ sách của máy sau 2 năm sử dụng, tức với x = 2 là: 

V(2) = 18 – 6 . 2 = 18 – 12 = 6 (triệu đồng).

d) Để có giá trị sổ sách là 9 triệu đồng thì V(x) = 9, tức là 9 = 18 – 6x, suy ra x = 1,5.

Vậy sau 1,5 năm sử dụng thì máy photocopy có giá trị sổ sách là 9 triệu đồng.