Bài 7.36 trang 56 Toán 8 Tập 2 Kết nối tri thức
Bài tập 7.36, trang 56 SGK Toán 8 Tập 2 (Kết nối tri thức), là bài tập cơ bản trong phần hàm số và đồ thị. Bài toán yêu cầu học sinh vẽ đồ thị của hai hàm số bậc nhất $y = 2x - 1$ và $y = -x + 2$ trên cùng một mặt phẳng tọa độ, sau đó tìm tọa độ giao điểm của chúng bằng phương pháp đại số.
Bài 7.36 trang 56 Toán 8 Tập 2 Kết nối tri thức:
Cho hai hàm số y = 2x – 1 và y = –x + 2.
a) Trong cùng mặt phẳng tọa độ Oxy, vẽ đồ thị của hai hàm số đã cho.
b) Tìm tọa độ giao điểm của hai đồ thị trên.
Phân tích và Phương pháp Giải
-
Vẽ đồ thị: Xác định hai điểm thuộc đồ thị của mỗi hàm số (thường là giao điểm với trục $Ox$ và $Oy$).
-
Tìm giao điểm: Giải phương trình hoành độ giao điểm $f(x) = g(x)$ để tìm $x$, sau đó thay $x$ vào một trong hai hàm số để tìm $y$.
Giải Bài 7.36 trang 56 Toán 8 Tập 2 Kết nối tri thức:
a) Đồ thị hàm số y = 2x – 1 là một đường thẳng đi qua hai điểm là (0; –1) và (1/2; 0)
Đồ thị hàm số y = –x + 2 là một đường thẳng đi qua hai điểm là (0; 2) và (2; 0).
Đồ thị của hai hàm số đã cho như hình sau:
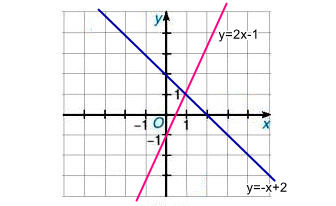
b) Phương trình hoành độ giao điểm của đồ thị hai hàm số là
2x – 1 = –x + 2
3x = 3
x = 1
Thay x = 1 vào hàm số y = 2x – 1, ta được y = 2 . 1 – 1 = 1.
Vậy tọa đô giao điểm của hai đồ thị hàm số trên là điểm A (1; 1).
Như vậy, ta có kết quả sau:
| Hàm số | Điểm đi qua | Kết luận về Giao điểm |
| $y = 2x - 1$ | $(0; -1), (0,5; 0)$ | Tọa độ giao điểm: $x = 1, y = 1$ |
| $y = -x + 2$ | $(0; 2), (2; 0)$ | Giao điểm là $A(1; 1)$ |
Giao điểm $A(1; 1)$ chính là nghiệm của hệ phương trình $\left\{\begin{matrix} y = 2x - 1 \\ y = -x + 2 \end{matrix}\right.$.
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 9.36 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.36 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.35 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.35 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.34 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.34 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.33 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.33 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.32 trang 109 Toán 8 Tập 2 Kết nối tri thức
Bài 9.32 trang 109 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.31 trang 107 Toán 8 Tập 2 Kết nối tri thức
Bài 9.31 trang 107 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.30 trang 107 Toán 8 Tập 2 Kết nối tri thức
Bài 9.30 trang 107 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.29 trang 107 Toán 8 Tập 2 Kết nối tri thức
Bài 9.29 trang 107 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.22 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.22 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.21 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.21 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.20 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.20 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.19 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.19 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.18 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.18 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 9.17 trang 97 Toán 8 Tập 2 Kết nối tri thức
Bài 9.17 trang 97 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.3 trang 62 Toán 8 Tập 2 Kết nối tri thức
Bài 8.3 trang 62 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.1 trang 62 Toán 8 Tập 2 Kết nối tri thức
Bài 8.1 trang 62 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.2 trang 62 Toán 8 Tập 2 Kết nối tri thức
Bài 8.2 trang 62 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.26 trang 77 Toán 8 Tập 2 Kết nối tri thức
Bài 8.26 trang 77 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.25 trang 77 Toán 8 Tập 2 Kết nối tri thức
Bài 8.25 trang 77 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.24 trang 77 Toán 8 Tập 2 Kết nối tri thức
Bài 8.24 trang 77 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.23 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.23 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.22 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.22 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.21 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.21 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.20 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.20 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.19 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.19 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.18 trang 76 Toán 8 Tập 2 Kết nối tri thức
Bài 8.18 trang 76 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.17 trang 75 Toán 8 Tập 2 Kết nối tri thức
Bài 8.17 trang 75 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.16 trang 75 Toán 8 Tập 2 Kết nối tri thức
Bài 8.16 trang 75 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.15 trang 75 Toán 8 Tập 2 Kết nối tri thức
Bài 8.15 trang 75 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 8.14 trang 75 Toán 8 Tập 2 Kết nối tri thức
Bài 8.14 trang 75 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.45 SGK Toán 8 Tập 2 Kết nối tri thức
Bài 7.45 SGK Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.44 SGK Toán 8 Tập 2 Kết nối tri thức
Bài 7.44 SGK Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.43 SGK Toán 8 Tập 2 Kết nối tri thức
Bài 7.43 SGK Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.42 SGK Toán 8 Tập 2 Kết nối tri thức
Bài 7.42 SGK Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.41 SGK Toán 8 Tập 2 Kết nối tri thức
Bài 7.41 SGK Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.47 trang 57 Toán 8 Tập 2 Kết nối tri thức
Bài 7.47 trang 57 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.46 trang 57 Toán 8 Tập 2 Kết nối tri thức
Bài 7.46 trang 57 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.45 trang 57 Toán 8 Tập 2 Kết nối tri thức
Bài 7.45 trang 57 Toán 8 Tập 2 Kết nối tri thức
-
 Bài 7.44 trang 57 Toán 8 Tập 2 Kết nối tri thức
Bài 7.44 trang 57 Toán 8 Tập 2 Kết nối tri thức


















































