Hotline 0936685849

Bài 5 trang 74 Toán 11 tập 2 Chân trời sáng tạo: Hình chóp cụt tứ giác đều

11:26:3806/02/2024

Bài 5 trang 74 Toán 11 Tập 2 thuộc chương 8 "Quan hệ vuông góc trong không gian". Bài tập này giúp các em củng cố kiến thức về hình chóp cụt tứ giác đều và cách tính các yếu tố hình học của nó, đặc biệt là độ dài cạnh bên và đường cao của mặt bên.

Đề bài

Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ và đường nối tâm hai đáy bằng a. Tính độ dài cạnh bên và đường cao của mỗi mặt bên.

Phân tích kiến thức và hướng dẫn giải chi tiết

1. Phương pháp giải

Để giải bài toán này, ta sẽ sử dụng định lí Pytago trong các mặt cắt vuông góc của hình chóp cụt.

Cạnh bên: Ta tạo một tam giác vuông có một cạnh là cạnh bên, một cạnh là chiều cao hình chóp cụt và cạnh còn lại là hình chiếu của cạnh bên lên mặt phẳng đáy.
Đường cao mặt bên: Ta tạo một tam giác vuông có một cạnh là đường cao mặt bên, một cạnh là chiều cao hình chóp cụt và cạnh còn lại là hình chiếu của đường cao mặt bên lên mặt phẳng đáy.

2. Lời giải chi tiết bài 5 trang 74 Toán 11

Ta có hình minh hoạ như sau:

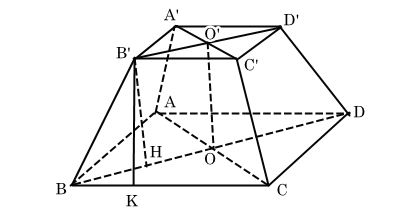
Giải bài 5 trang 74 Toán 11 tập 2 Chân trời sáng tạo

Gọi $A BC D$ là đáy lớn và $A^{'} B^{'} C^{'} D^{'}$ là đáy nhỏ. $O, O^{'}$ lần lượt là tâm của hai đáy. Ta có: Cạnh đáy lớn $A B = 2 a$ . Cạnh đáy nhỏ $A^{'} B^{'} = a$ . Chiều cao hình chóp cụt $O O^{'} = a$ .

a) Tính độ dài cạnh bên $B B^{'}$

Bước 1: Tính độ dài các đường chéo của hai đáy.

$BD=\sqrt{AB^2+AD^2}=\sqrt{(2a)^2+(2a)^2}=2a\sqrt{2}$

$B'D'=\sqrt{A'B'^2+A'D'^2}=\sqrt{a^2+a^2}=a\sqrt{2}$
Bước 2: Tính hình chiếu của cạnh bên lên mặt phẳng đáy.

Gọi $H$ là hình chiếu của $B^{'}$ lên đường chéo $B D$ . Khi đó $B^{'} H$ là chiều cao của hình chóp cụt, $B'H=OO'=a$ .

Khoảng cách từ tâm đến đỉnh của đáy lớn: $BO=\frac{BD}{2}=\frac{2a\sqrt{2}}{2}=a\sqrt{2}$

Khoảng cách từ tâm đến đỉnh của đáy nhỏ: $B'O'=\frac{B'D'}{2}=\frac{a\sqrt{2}}{2}$

Độ dài đoạn $B H$ là: $BH=BO-B'O'=a\sqrt{2}-\frac{a\sqrt{2}}{2}=\frac{a\sqrt{2}}{2}$
Bước 3: Áp dụng định lí Pytago trong $Δ B B^{'} H$ vuông tại $H$ .

$BB'^2=B'H^2+BH^2=a^2+(\frac{a\sqrt{2}}{2})^2=a^2+\frac{2a^2}{4}=a^2+\frac{a^2}{2}=\frac{3a^2}{2}$

$BB'=\sqrt{\frac{3a^2}{2}}=\frac{a\sqrt{3}}{\sqrt{2}}=\frac{a\sqrt{6}}{2}$

b) Tính đường cao của mỗi mặt bên

Bước 1: Kẻ đường cao B'K của mặt bên $BC C^{'} B^{'}$ , B'K là đường cao của hình thang cân $BC C^{'} B^{'}$ .
Bước 2: Tính độ dài hình chiếu của đường cao mặt bên lên mặt phẳng đáy.

Đây là một đoạn thẳng có độ dài bằng nửa hiệu của hai đáy của hình thang mặt bên. $\frac{BC-B'C'}{2}=\frac{2a-a}{2}=\frac{a}{2}$
Bước 3: Áp dụng định lí Pytago. Đường cao mặt bên KB' là cạnh huyền của tam giác vuông với các cạnh góc vuông là chiều cao của hình chóp cụt ( $a$ ) và nửa hiệu độ dài hai đáy của mặt bên ( $a/2$ ).

$B'K^2=a^2+(\frac{a}{2})^2=a^2+\frac{a^2}{4}=\frac{5a^2}{4}$

$B'K=\sqrt{\frac{5a^2}{4}}=\frac{a\sqrt{5}}{2}$

Đáp số:

Độ dài cạnh bên của hình chóp cụt là $\frac{a\sqrt{6}}{2}$

Độ dài đường cao của mỗi mặt bên là $\frac{a\sqrt{5}}{2}$

Bài toán này là một ví dụ điển hình về việc sử dụng định lí Pytago để giải các bài toán hình học không gian. Nắm vững cách dựng hình chiếu và xác định các tam giác vuông là chìa khóa để giải quyết bài toán một cách chính xác. Chúc các em học tốt!

• Xem thêm Giải Toán 11 Tập 2 Chân trời sáng tạo SGK

> Bài 1 trang 73 Toán 11 tập 2 Chân trời sáng tạo: Cho hình chóp S.ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong...

> Bài 2 trang 73 Toán 11 tập 2 Chân trời sáng tạo: Cho tam giác đều ABC cạnh a, I trung điểm của BC, D là điểm đối xứng với A qua I. Vẽ đoạn thẳng...

> Bài 3 trang 73 Toán 11 tập 2 Chân trời sáng tạo: Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy ABCD là hình thang vuông tại A và B, AA′ = 2a...

> Bài 4 trang 74 Toán 11 tập 2 Chân trời sáng tạo: Cho hình hộp ABCD.A′B′C′D′ có đáy là hình thoi. Cho biết AB = BD = a, A′C = 2a...

> Bài 5 trang 74 Toán 11 tập 2 Chân trời sáng tạo: Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ và đường nối tâm hai đáy...

> Bài 6 trang 74 Toán 11 tập 2 Chân trời sáng tạo: Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m...