Hotline 0936685849

Bài 3 trang 73 Toán 11 tập 2 Chân trời sáng tạo: Hình Lăng Trụ Đứng & Hình Học Không Gian

10:25:0606/02/2024

Bài 3 trang 73 Toán 11 Tập 2 thuộc chương "Hệ tọa độ trong không gian". Bài tập này giúp các em củng cố kiến thức về hình học không gian, đặc biệt là cách tính độ dài đường chéo và diện tích các mặt của một hình lăng trụ đứng có đáy là hình thang vuông.

Đề bài

Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy ABCD là hình thang vuông tại A và B, AA′ = 2a, AD = 2a, AB = BC = a.

a) Tính độ dài đoạn thẳng AC′.

b) Tính tổng diện tích các mặt của hình lăng trụ.

Phân tích kiến thức và hướng dẫn giải chi tiết

1. Phương pháp giải

Để giải bài toán này, chúng ta cần thực hiện các bước sau:

Tính độ dài đoạn thẳng: Sử dụng định lí Pytago trong tam giác vuông để tính độ dài các cạnh và đường chéo.
Tính tổng diện tích các mặt: Tổng diện tích các mặt của hình lăng trụ bằng tổng diện tích xung quanh và diện tích hai đáy.

$S_{tp}=S_{xq}+2S_{d}$

2. Lời giải chi tiết bài 3 trang 73 Toán 11

Ta có hình minh hoạ như sau:

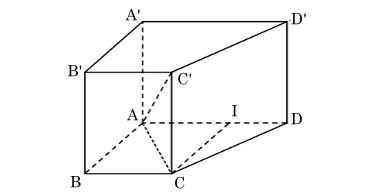
Giải bài 3 trang 73 Toán 11 tập 2 Chân trời sáng tạo

a) Tính độ dài đoạn thẳng AC′.

Ta có: $\dpi{100} AC=\sqrt{AB^2+BC^2}$ $=\sqrt{a^2+a^2}=a\sqrt{2}$

$\Rightarrow A'C=\sqrt{AC^2+CC'^2}$ $=\sqrt{(a\sqrt{2})^2+(2a)^2}=a\sqrt{6}$

Vậy độ dài đoạn thẳng AC′ là $a\sqrt{6}$

b) Tính tổng diện tích các mặt của hình lăng trụ.

Ta có:

$S_{ABCD}=S_{A'B'C'D'}=\frac{1}{2}(AD+BC).AB$ $=\frac{1}{2}(2a+a).a=\frac{3}{2}a^2$

Gọi I là trung điểm của AD.

Khi đó ABCI là hình vuông nên:

IC = IB = IA = AD/2 = a

Xét tam giác ICD vuông cân tại I:

$CD=\sqrt{CI^2+DI^2}=\sqrt{a^2+a^2}=a\sqrt{2}$

S_ABB'A' = AB.AA' = a.2a = 2a²

S_ADD'A' = AD.AA' = 2a.2a = 4a²

S_BCB'C' = BC.CC' = a.2a = 2a²

S_CDD'C' = CD.CC' = a $\sqrt{2}$ .2a = 2 $\sqrt{2}$ a²

Tổng diện tích các mặt của hình lăng trụ là:

S = S_ABCD + S_A'B'C'D' + S_ABB'A' + S_ADD'A' + S_BCB'C' + S_CDD'C'

= 1,5a² + 1,5a² + 2a² + 4a² + 2a² + 2 $\sqrt{2}$ a² = (11 + 2 $\sqrt{2}$ )a²

Vậy tổng diện tích các mặt của hình lăng trụ là:(11 + 2 $\sqrt{2}$ )a²

Tổng kết và lời khuyên

Đáp số:

a) Độ dài đoạn thẳng $A C^{'}$ là $a\sqrt{6}$ .

b) Tổng diện tích các mặt của hình lăng trụ là (11 + 2 $\sqrt{2}$ )a².

Bài toán này giúp các em làm quen với việc tính toán trong hình học không gian. Nắm vững các công thức tính toán độ dài, diện tích và sử dụng định lí Pytago là chìa khóa để giải quyết các bài toán một cách dễ dàng và chính xác. Chúc các em học tốt!

• Xem thêm Giải Toán 11 Tập 2 Chân trời sáng tạo SGK

> Bài 1 trang 73 Toán 11 tập 2 Chân trời sáng tạo: Cho hình chóp S.ABC có đáy là tam giác vuông tại C, mặt bên SAC là tam giác đều và nằm trong...

> Bài 2 trang 73 Toán 11 tập 2 Chân trời sáng tạo: Cho tam giác đều ABC cạnh a, I trung điểm của BC, D là điểm đối xứng với A qua I. Vẽ đoạn thẳng...

> Bài 3 trang 73 Toán 11 tập 2 Chân trời sáng tạo: Cho hình lăng trụ đứng ABCD.A′B′C′D′ có đáy ABCD là hình thang vuông tại A và B, AA′ = 2a...

> Bài 4 trang 74 Toán 11 tập 2 Chân trời sáng tạo: Cho hình hộp ABCD.A′B′C′D′ có đáy là hình thoi. Cho biết AB = BD = a, A′C = 2a...

> Bài 5 trang 74 Toán 11 tập 2 Chân trời sáng tạo: Cho hình chóp cụt tứ giác đều có cạnh đáy lớn bằng 2a, cạnh đáy nhỏ và đường nối tâm hai đáy...

> Bài 6 trang 74 Toán 11 tập 2 Chân trời sáng tạo: Kim tự tháp bằng kính tại bảo tàng Louvre ở Paris có dạng hình chóp tứ giác đều với chiều cao là 21,6 m...