Bài 1.46 trang 44 Toán 12 tập 1 Kết nối tri thức

Bài 1.46 trang 44 Toán 12 Tập 1 Kết nối tri thức:

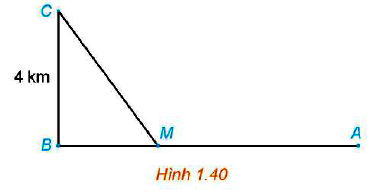
Một đường dây điện được nối từ một nhà máy điện ở A đến một hòn đảo ở C như Hình 1.40. Khoảng cách từ C đến B là 4km. Bờ biển chạy thẳng từ A đến B với khoảng cách là 10km. Tổng chi phí lắp đặt cho 1km dây điện trên biển là 50 triệu đồng, còn trên đất liền là 30 triệu đồng. Xác định vị trí điểm M trên đoạn AB (điểm nối dây từ đất liền ra đảo) để tổng chi phí lắp đặt là nhỏ nhất.

Giải bài 1.46 trang 44 Toán 12 Tập 1 Kết nối tri thức:

Đặt MB = x (km, 0 ≤ x ≤ 10)

Khi đó: Am = 10 - x (km)

và  (km)

Khi đó, chi phí nối điện từ A đến C là:

 (triệu đồng)

Ta có:  

⇔ 25x² = 9x² + 144 ⇔ x = 3 (vì 0 ≤ x ≤ 10)

Ta có: f(0) = 500; f(3) = 460; f(10) = 100 nên chi phí nhỏ nhất là 460 triệu đồng khi x = 3

Vậy M cách B một khoảng 3km trên đoạn AB (điểm nối dây từ đất liền ra đảo) thì tổng chi phí lắp đặt là nhỏ nhất.