Giải bài 10 trang 48 SGK Toán 9 tập 1: Cách lập công thức y theo x

Đề bài:

Một hình chữ nhật có các kích thước là 20cm và 30cm. Người ta bớt mỗi kích thước của nó đi x (cm) được hình chữ nhật mới có chu vi là y (cm). Hãy lập công thức tính y theo x.

Phân tích và Hướng dẫn giải

Để lập công thức tính $y$ theo $x$, ta thực hiện các bước sau:

1. Xác định kích thước mới của hình chữ nhật sau khi bớt đi $x$ cm.

2. Sử dụng công thức tính chu vi của hình chữ nhật: $C=2(a+b)$ Trong đó, $a$ và $b$ là chiều dài và chiều rộng của hình chữ nhật.

3. Thay thế các kích thước mới vào công thức chu vi để lập được công thức tính $y$ theo $x$.

Lời giải chi tiết bài 10 trang 48 Toán 9:

- Gọi hình chữ nhật ban đầu ABCD có kích thước AB = 30cm; BC = 20cm như hình minh hoạ như sau:

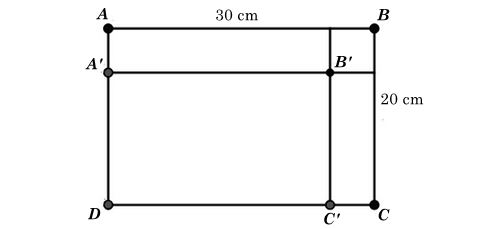
- Sau khi bớt các kích thước của hình chữ nhật đi x (cm) (giả sử bớt AB và BC), ta có hình chữ nhật mới là A'B'C'D có:

A'B' = 30 – x

B'C' = 20 – x

Gọi y là chu vi của hình chữ nhật A'B'C'D, ta có:

y = 2[(30 – x) + (20 – x)]

y = 2(50 – 2x)

y = –4x + 100 (cm).

Vậy công thức tính y theo x là: y = –4x + 100 (cm)