Tìm GTNN, GTLN của biểu thức chứa giá trị tuyệt đối

Bài viết dưới đây hướng dẫn các em cách tìm GTNN, GTLN (giá trị nhỏ nhất, giá trị lớn nhất) của biểu thức chứa giá trị tuyệt đối lớp 9 qua một số bài tập minh họa cụ thể.

Tìm GTNN, GTLN (giá trị nhỏ nhất nhất, giá trị lớn nhất) của biểu thức chứa dấu giá trị tuyệt đối

* Phương pháp: (đối với biểu thức 1 biến số)

Bài toán này cũng chủ yếu dựa vào tính không âm của trị tuyệt đối.

* Ví dụ 1: Tìm GTLN của biểu thức: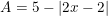 

° Lời giải:

- Ta có: |2x - 2| ≥ 0 ⇔ -|2x - 2| ≤ 0 ⇔ 5 -|2x - 2| ≤ 5

 Dấu "=" xảy ra khi |2x - 2| = 0 ⇔ 2x - 2 = 0 ⇔ x = 1

 Vậy A_max = 5 ⇔ x = 1

* Ví dụ 2: Tìm GTNN của biểu thức: A = |9 - x| - 3

° Lời giải:

- Ta có: |9 - x| ≥ 0 ⇔ |9 - x| ≥ 0 ⇔ |9 - x| - 3 ≥ -3

Dấu "=" xảy ra khi |9 - x| = 0 ⇔ 9 - x = 0 ⇔ x = 9

 Vậy A_min = -3 ⇔ x = 9

Như vậy, các bài toán trên dựa trên các biến đổi về dạng tổng hoặc hiệu của biểu thức không âm (bình phương, trị tuyệt đối,...) và hằng số để tìm ra lời giải.

Thực tế, còn nhiều bài toán phải sử dụng bất đẳng thức Cauchy (Cosi) cho hai số a, b không âm: 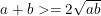 (Dấu "=" xảy ra khi a =b) hay áp dụng bất đẳng thức chứa dấu giá trị tuyệt đối:  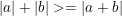(dấu "=" xảy ra khi và chỉ khi a.b≥ 0); 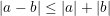, (dấu "=" xảy ra khi và chỉ khi a.b≤ 0).

* Ví dụ 1: Tìm giá trị nhỏ nhất (GTNN) của biểu thức:

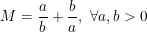
° Lời giải:

-  Vì a, b > 0 nên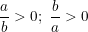 

- Áp dụng bất đẳng thức Cauchy (còn gọi là bất đẳng thức so sánh giữa trung bình cộng và trung bình nhân AM-GM (Arithmetic Means - Geometric Means)).

 Dấu "=" xảy ra khi 

- Kết luận: Giá trị nhỏ nhất của M = 2 ⇔ a = b.

* Ví dụ 2: Tìm giá trị nhỏ nhất (GTNN) của biểu thức:

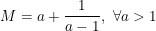
° Lời giải:

-  Vì a > 1 nên a - 1 > 0 ta có:

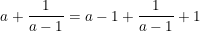  (Áp dụng bất đẳng thức Cauchy ta được)

Dấu "=" xảy ra khi:

Đối chiếu điều kiện a > 1 nên chỉ nhận a = 2; loại a = 0.

- Kết luận: GTNN của M = 3 ⇔ a = 2.