Giải bài 3 trang 29 Toán 10 tập 1 SGK Cánh Diều

Đề bài:

Miền không bị gạch trong mỗi Hình 12a, 12b là miền nghiệm của hệ bất phương trình nào cho ở dưới đây?

a) 

b)

c)

Phân tích và Hướng dẫn giải:

Để xác định hệ bất phương trình từ miền nghiệm không bị gạch, ta thực hiện các bước:

1. Tìm phương trình các đường thẳng ranh giới: Dùng tọa độ các điểm đi qua để xác định phương trình $d_i: ax + by = c$.

2. Xác định dấu bất đẳng thức:

   • Chọn một điểm kiểm tra $M(x_0; y_0)$ nằm trong miền không gạch (miền nghiệm).

   • Thay tọa độ $M$ vào biểu thức $ax + by$ và so sánh với $c$ để xác định dấu $>, <, \ge, \le$.

   • Vì các đường thẳng trong hình là nét liền (kể cả biên), nên dấu bất đẳng thức phải là $\le$ hoặc $\ge$.

Lời giải chi tiết:

• Quan sát Hình 12a, đặt tên các đường thẳng như trên hình:

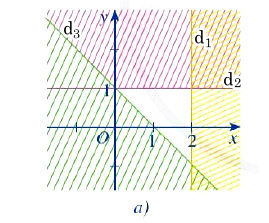+ Đường thẳng d₁ đi qua điểm (2; 0) và song song với trục tung, do đó phương trình đường thẳng d₁: x = 2.

+ Đường thẳng d₂ đi qua điểm (1; 0) và song song với trục hoành, do đó phương trình đường thẳng d₂: y = 1.

+ Giả sử d₃: y = ax + b (a ≠ 0)

Ta thấy đường thẳng d₃ đi qua 2 điểm (0; 1) và (1; 0). Thay tọa độ của mỗi điểm vào phương trình ta được: b = 1 và a + b = 0. Suy ra a = – 1 (t/m) và b = 1.

Khi đó, d₃: y = – x + 1. 

Do đó, ta thấy phần không gạch sọc trên hình chính là miền nghiệm của hệ c)

• Quan sát Hình 12b, đặt tên các đường thẳng như hình:

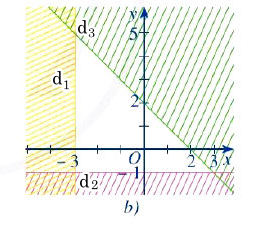+ Đường thẳng d₁ đi qua điểm (–3; 0) và song song với trục tung nên d₁: x = –3.

+ Đường thẳng d₂ đi qua điểm (0; –1) và song song với trục hoành nên d₂: y = –1.

+ Đường thẳng d₃ đi qua hai điểm (2; 0) và (0; 2).

Giả sử d₃: y = ax + b (a ≠ 0)

Thay tọa độ các điểm (2; 0) và (0; 2) vào phương trình đường thẳng ta tìm được a = – 1 (t/m) và b = 2.

Khi đó, d₃: y = – x + 2 ⇔ x + y = 2.

 Do đó, ta thấy phần không gạch sọc trên hình chính là miền nghiệm của hệ a)