Giải bài 2 trang 47 Toán 11 tập 1 SGK Cánh Diều

Đề bài:

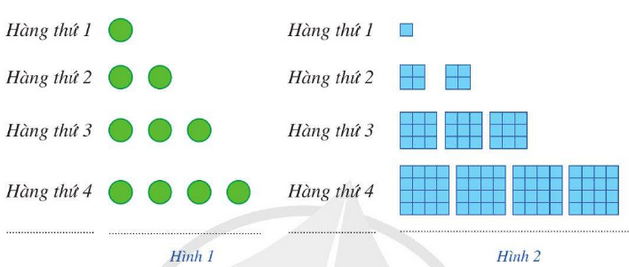
a) Gọi u_n là số chấm ở hàng thứ n trong Hình 1. Dự đoán công thức số hạng tổng quát cho dãy số (u_n).

b) Gọi v_n là tổng diện tích của các hình tô màu ở hàng thứ n trong Hình 2 (mỗi ô vuông nhỏ là một đơn vị diện tích). Dự đoán công thức của số hạng tổng quát cho dãy số (v_n).

Phân tích và Hướng dẫn giải:

Ta tiến hành phân tích mối quan hệ giữa chỉ số $n$ và giá trị của số hạng $u_n$ (hoặc $v_n$):

1. Xác định các số hạng đầu tiên ($u_1, u_2, u_3, \dots$) hoặc ($v_1, v_2, v_3, \dots$).

2. Tìm quy luật: Quan sát xem giá trị của số hạng có phải là bội số, lũy thừa, hoặc một hàm đơn giản nào đó của chỉ số $n$ hay không.

3. Dự đoán công thức tổng quát $u_n$ hoặc $v_n$ theo $n$.

Lời giải chi tiết:

a) Số chấm ở hàng thứ nhất là: u₁ = 1;

Số chấm ở hàng thứ hai là: u₂ = 2;

Số chấm ở hàng thứ ba là: u₃ = 3;

Số chấm ở hàng thứ tư là: u₄ = 4;

⇒ Số chấm ở hàng thứ n là: u_n = n.

b) Diện tích của các ô màu ở hàng thứ nhất là: v₁ = 1 = 1³;

Diện tích của các ô màu ở hàng thứ hai là: v₂ = 8 = 2³;

Diện tích của các ô màu ở hàng thứ ba là: v₃ = 27 = 3³;

Diện tích của các ô màu ở hàng thứ tư là: v₄ = 64 = 4³;

⇒ Diện tích của các ô màu ở hàng thứ n là: v_n = n³.