Hotline 0962 782 149

Chứng minh biểu thức lượng giác không phụ thuộc vào biến - Toán 10 chuyên đề

19:16:2523/07/2022

Là một trong những dạng toán lượng giác lớp 10, chứng minh biểu thức lượng giác không phụ thuộc vào biến là một trong những dạng bài tập mà chúng ta cũng hay gặp.

Vậy cách chứng minh biểu thức lượng giác không phụ thuộc vào biến như thế nào? cùng hay-học-hỏi.vn tìm hiểu qua bài viết dưới đây và vận dụng vào giải một số bài tập vận dụng nhé.

» Đừng bỏ lỡ: Đầy đủ các dạng toán phương trình lượng giác và cách giải hay

* Để giải dạng bài tập: chứng minh biểu thức lượng giác không phụ thuộc vào biến chúng ta cần vận dụng các công thức và thực hiện các phép biến đổi lượng giác.

* Ví dụ 1: Chứng minh các biểu thức sau không phụ thuộc x:

a) 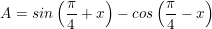$small A=sinleft ( frac{pi }{4}+x ight )-cosleft ( frac{pi }{4}-x ight )$

b) 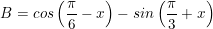$small B=c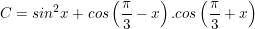osleft ( frac{pi }{6}-x ight )-sinleft ( frac{pi }{3}+x ight )$

c) $small C=sin^2x+cosleft ( frac{pi }{3}-x ight ).cosleft ( frac{pi }{3}+x ight )$

d) 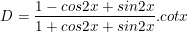$small D=frac{1-cos2x+sin2x}{1+cos2x+sin2x}.cotx$

° Lời giải:

a) Ta có:

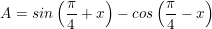
$small A=sinleft ( frac{pi }{4}+x ight )-cosleft ( frac{pi }{4}-x ight )$

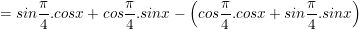
$small =sinfrac{pi }{4}.cosx+cosfrac{pi }{4}.sinx-left ( cosfrac{pi }{4}.cosx+sinfrac{pi }{4}.sinx ight )$

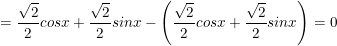
$small =frac{sqrt{2}}{2}cosx+frac{sqrt{2}}{2}sinx-left ( frac{sqrt{2}}{2}cosx+frac{sqrt{2}}{2}sinx ight )=0$

⇒ Vậy biểu thức A=0 không phụ thuộc vào giá trị của x

b) Ta có:

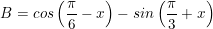
$small B=cosleft ( frac{pi }{6}-x ight )-sinleft ( frac{pi }{3}+x ight )$

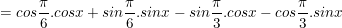
$small =cosfrac{pi }{6}.cosx+sinfrac{pi }{6}.sinx-sinfrac{pi }{3}.cosx-cosfrac{pi }{3}.sinx$

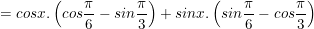
$small =cosx.left ( cosfrac{pi }{6}-sinfrac{pi }{3} ight )+sinx.left ( sinfrac{pi }{6}-cosfrac{pi }{3} ight )$

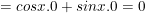
small =cosx.0+sinx.0=0

(vì 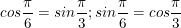$small cosfrac{pi }{6}=sinfrac{pi }{3};sinfrac{pi }{6}=cosfrac{pi }{3}$ )

⇒ Vậy biểu thức B=0 không phụ thuộc vào giá trị của x

c) Ta có:

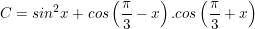
$small C=sin^2x+cosleft ( frac{pi }{3}-x ight ).cosleft ( frac{pi }{3}+x ight )$

$small =sin^2x+left [ cosfrac{pi }{3}.cosx +sinfrac{pi }{3}.sinx ight ]left [ cosfrac{pi }{3}.cosx-sinfrac{pi }{3}.sinx ight ]$

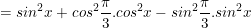
$small =sin^2x+cos^2frac{pi }{3}.cos^2x-sin^2frac{pi }{3}.sin^2x$

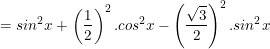
$small =sin^2x+left ( frac{1}{2} ight )^2.cos^2x-left (frac{sqrt{3}}{2} ight )^2.sin^2x$

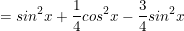
$small =sin^2x+frac{1}{4}cos^2x-frac{3}{4}sin^2x$

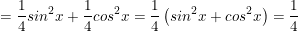
$small =frac{1}{4}sin^2x+frac{1}{4}cos^2x=frac{1}{4}left ( sin^2x+cos^2x ight )=frac{1}{4}$

⇒ Vậy biểu thức C=1/4 không phụ thuộc vào giá trị của x

d) Ta có:

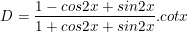
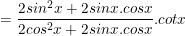
$small D=frac{1-cos2x+sin2x}{1+cos2x+sin2x}.cotx$ $small =frac{2sin^2x+2sinx.cosx}{2cos^2x+2sinx.cosx}.cotx$

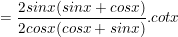
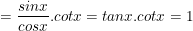
$small =frac{2sinx(sinx+cosx)}{2cosx(cosx+sinx)}.cotx$ $small =frac{sinx}{cosx}.cotx=tanx.cotx=1$

⇒ Vậy biểu thức D=1 không phụ thuộc vào giá trị của x.

* Ví dụ 2: Chứng minh các biểu thức lượng giác sau không phụ thuộc vào biến x:

a) cos²(α + x) + cos²x - 2cosαcosx.cos(α + x)

b) sin4x.sin10x - sin11x.sin3x - sin7x.sinx

* Lời giải:

a) cos²(α + x) + cos²x - 2cosαcosx.cos(α + x)

- Ta có:

cos²(α + x) + cos²x - 2cosαcosx.cos(α + x)

= cos(α + x)[cos(α + x) - 2cosαcosx] + cos²x

= cos(α + x)(-cosα.cosx - sinα.sinx) + cos²x

= -cos(α + x)cos(α - x) + cos²x

$\small =-\frac{1}{2}(cos2\alpha +cos2x)+cos^2x$

$\small =-\frac{cos2\alpha}{2} -\frac{cos2x}{2}+cos^2x$

$\small =-\frac{1}{2}cos2\alpha +\frac{1}{2}=sin^2\alpha$

Vậy biểu thức lượng giác trên không phụ thuộc vào x

b) sin4x.sin10x - sin11x.sin3x - sin7x.sinx

- Ta có:

sin4x.sin10x - sin11x.sin3x - sin7x.sinx

$\small =\frac{1}{2}(cos6x-cos14x)-\frac{1}{2}(cos8x-cos14x)$ $\small -\frac{1}{2}(cos6x-cos8x)$

$\small =\frac{1}{2}(cos6x-cos14x-cos8x+cos14x$ $\small -cos6x+cos8x)$

= 0.

Vậy biểu thức trên không phụ thuộc vào biến x.

Hy vọng với bài viết về Chứng minh biểu thức lượng giác không phụ thuộc vào biến Toán lớp 10 ở trên giúp ích cho các em. Mọi góp ý và thắc mắc các em hãy để lại phần bình luận dưới bài viết để Hay-Học-Hỏi.Vn ghi nhận và hỗ trợ, chúc các em học tập tốt.

Chứng minh biểu thức lượng giác không phụ thuộc vào biến - Toán 10 chuyên đề

Tags:

Đánh giá & nhận xét