Cách giải bất phương trình tích và bài tập vận dụng - Toán 10 chuyên đề

Vậy cách giải phương trình tích như thế nào? cùng hayhọchỏi.vn tìm hiểu qua bài bài viết dưới đây và vận dụng vào giải một số bài tập minh họa về bất phương trình tích để hiểu rõ hơn dạng toán này nhé các em.

I. Cách giải Bất phương trình tích

Để giải các bất phương trình tích dạng: 

P(x) > 0, P(x) < 0, P(x) ≥ 0, P(x) ≤ 0.

trong đó P(x) = (a₁x + b₁)(a₂x + b₂)+ ... + (a_nx + b_n) là tích những nhị thức bậc nhất được thực hiện theo các bước:

+ Bước 1: Tìm các nghiệm x₁, ... , x_n của các nhị thức a₁x + b₁ , ... , a_nx + b_n.

+ Bước 2: Sắp xếp các nghiệm theo thứ tự tăng dần (giả sử x_k < ... < x_l) từ đó lập bảng xét dấu dạng như sau:

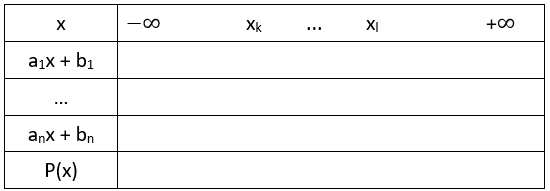
+ Bước 3: Dựa vào bảng xét dấu kết luận nghiệm của bất phương trình.

II. Bài tập giải Bất phương trình tích

* Bài tập 1: Giải bất phương trình tích sau:

* Lời giải:

Ta có: 2x – 1 = 0 ⇔ x = 1/2;

 x + 3 = 0 ⇔ x = –3.

Ta lập được bảng xét dấu như sau:

Từ bảng xét dấu ta thấy: 

 Vậy tập nghiệm của bất phương trình là: S = [-3;1/2]

Ta có:

 –3x – 3 = 0 ⇔ x = –1;

 x + 2 = 0 ⇔ x = –2;

 x + 3 = 0 ⇔ x = –3.

Ta lập được bảng xét dấu sau:

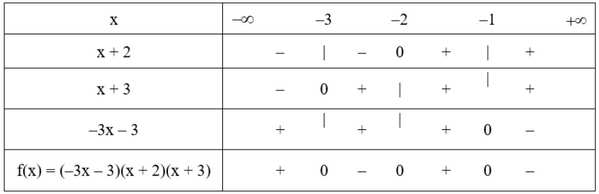
Từ bảng xét dấu ta thấy: 

 Vậy tập nghiệm của bất phương trình là: S = (-∞; -3] U [-2 ; -1]

- Ta có: f(x) = 4x² – 1 = (2x + 1)(2x – 1)

Suy ra f(x) = 0 ⇔ x = 1/2 hoặc x = -1/2.

Ta lập được bảng xét dấu sau:

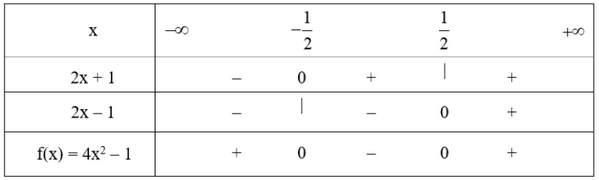
Từ bảng xét dấu ta thấy:  

Vậy tập nghiệm của bất phương trình là: S = (-∞;-1/2] U [1/2; +∞)

* Bài tập 2: Giải các phương trình tích sau:

a) (3x² - 10x + 3)(4x - 5) > 0

b) (3x² - 4x)(2x² - x - 1) < 0

c) (4x² - 1)(-8x² + x - 3)(2x + 9) ≥ 0

d) (2x - 3)(x + 5)(3x - 15) ≤ 0

* Bài tập 3: Giải các phương trình