Cách giải bất phương trình chứa dấu giá trị tuyệt đối và Bài tập - Toán 10 chuyên đề

Vậy cụ thể, cách giải bất phương trình chứa dấu trị tuyệt đối như thế nào? cùng hayhọchỏi tìm hiểu qua bài bài viết này và vận dụng vào giải một số bài tập minh họa để hiểu rõ hơn nhé các em.

I. Cách giải Bất phương trình chứa dấu trị tuyệt đối

• Một số tính chất của trị tuyệt đối

Điều kiện a > 0

i) |x| ≥ 0, |x| ≥ x, |x| ≥ -x

ii) |x| ≤ a ⇔ -a ≤ x ≤ a

iii) |x| ≥ a ⇔ x ≤ -a hoặc x ≥ a

iv) |a| - |b| ≤ |a + b| ≤ |a| + |b| 

• Định nghĩa trị tuyệt đối:

 |f(x)| = f(x) khi f(x) ≥ 0.

 |f(x)| = -f(x) khi f(x) < 0.

• Bất phương trình chứa dấu giá trị tuyệt đối thường gặp 2 dạng cơ bản sau:

i) |f(x)| > g(x) hoặc |f(x)| < g(x)

°   hoặc 

° 

 hoặc

ii) |f(x)| > |g(x)| hoặc |f(x)| < |g(x)|

°  

• Để giải bất phương trình chứa dấu giá trị tuyệt đối ta thực hiện các bước sau:

+ Bước 1: Đặt điều kiện có nghĩa cho các biểu thức trong bất phương trình

+ Bước 2: Phá dấu trị tuyệt đối (bằng cách dùng định nghĩa trị tuyệt đối, tính chất của trị tuyệt đối, lập bảng xét dấu cho các biểu thức chứa dấu trị tuyệt đối, hoặc bình phương 2 vế,...)

+ Bước 3: Giải bất phương trình trên mỗi khoảng đã chia

+ Bước 4: Kết luận nghiệm phương trình.

II. Bài tập giải bất phương trình chứa dấu trị tuyệt đối

* Bài tập 1: Giải bất phương trình chứa dấu trị tuyệt đối sau:

* Lời giải:

Vậy tập nghiệm của bất phương trình là: 

- Điều kiện xác định: x ≠ 1; x ≠ –2.

Bình phương hai vế ta được:

⇔ 25(x - 1)² < 100(x + 2)²

⇔ x² - 2x + 1 < 4(x² + 4x + 4)

⇔ 3x² + 18x + 15 > 0

⇔ x² + 6x + 5 > 0

⇔ (x + 1)(x + 5) > 0

Ta có bảng xét dấu: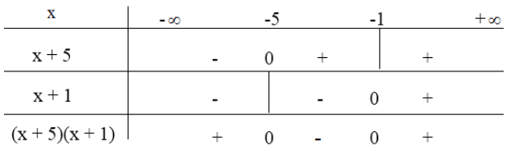

Dựa vào bảng xét dấu ta thấy (x + 1)(x + 5) > 0 khi x < -5 hoặc x > -1.

Kết hợp điều kiện x ≠ 1; x ≠ -2 vậy tập nghiệm của bất phương trình là:

S = (–∞; -5)∪(-1; +∞)\{1}.

* Bài tập 2: Giải các bất phương trình có chứa dấu trị tuyệt đối sau:

a) |2x - 9| ≤ x + 2.

b) |2x - 3| ≥ x + 2.

* Lời giải:

a) |2x - 9| ≤ x + 2.

Vậy tập nghiệm của phương trình là: S = [7/3;11]

b) |2x - 3| ≥ x + 2.

Vậy tập nghiệm của phương trình là:  S = (-∞;1/3]U[5; ∞)