Bài 7.36 trang 64 Toán 11 tập 2 Kết nối tri thức

Bài 7.36 trang 64 Toán 11 Tập 2 Kết nối tri thức:

Cho hình chóp S.ABCD có đáy ABCD là hình vuông và SA ⊥ (ABCD).

Phát biểu nào sau đây là sai?

A. Đường thẳng BC vuông góc với mặt phẳng (SAB).

B. Đường thẳng BD vuông góc với mặt phẳng (SAC).

C. Đường thẳng AC vuông góc với mặt phẳng (SBD).

D. Đường thẳng AD vuông góc với mặt phẳng (SAB).

Giải bài 7.36 trang 64 Toán 11 Tập 2 Kết nối tri thức:

* Đáp án: C.

Vì, ta có:

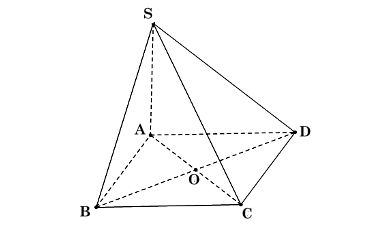
Vì ABCD là hình vuông nên AB ⊥ BC mà SA ⊥ (ABCD) nên SA ⊥ BC.

Có AB ⊥ C và SA ⊥ BC nên BC ⊥ (SAB).

⇒ A đúng.

Vì ABCD là hình vuông nên AC ⊥ BD mà SA ⊥ (ABCD) nên SA ⊥ BD.

Có AC ⊥ BD và SA ⊥ BD nên BD  ⊥ (SAC).

⇒  B đúng.

Vì ABCD là hình vuông nên AD ⊥ AB mà SA ⊥ (ABCD) nên SA ⊥ AD.

Có AD ⊥ AB và SA ⊥ AD nên AD ⊥ (SAB).

⇒ D đúng.