Bài 7.35 trang 64 Toán 11 tập 2 Kết nối tri thức

Bài 7.35 trang 64 Toán 11 Tập 2 Kết nối tri thức:

Cho hình chóp tứ giác đều S.ABCD. Phát biểu nào sau đây là đúng?

A. Số đo của góc nhị diện [S, AB, C] bằng 

B. Số đo của góc nhị diện [D, SA, B] bằng 90°.

C. Số đo của góc nhị diện [S, AC, B] bằng 90°.

D. Số đo của góc nhị diện [D, SA, B] bằng 

Giải bài 7.35 trang 64 Toán 11 Tập 2 Kết nối tri thức:

* Đáp án: C.

Vì, ta có:

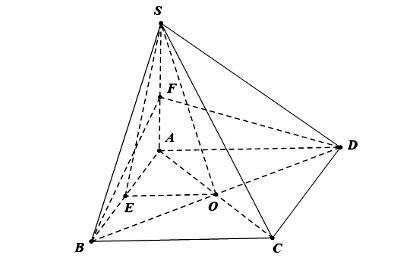
Gọi O là giao điểm của AC và BD.

Kẻ OE ⊥ AB tại E.

Vì ABCD là hình vuông nên O là trung điểm của AC và BD.

Xét tam giác ABD có OE // AD (do cùng vuông góc với AB) mà O là trung điểm của BD nên E là trung điểm của AB.

Xét tam giác SAB có SA = SB (do S.ABCD là hình chóp tứ giác đều) nên SAB là tam giác cân tại S mà SE là trung tuyến nên SE đồng thời là đường cao hay SE ⊥ AB.

Do đó [S, AB, C] = ,

⇒ A sai.

Vì ABCD là hình vuông nên BO ⊥ AC, S.ABCD là hình chóp đều nên SO ⊥ (ABCD)

suy ra SO ⊥ AC, SO ⊥ BD .

Vì BO ⊥ AC, SO ⊥ AC nên [S, AC, B] =  = 90^o,

⇒ C đúng.

Kẻ DF ⊥ SA tại F.

Vì SO ⊥ BD và AC ⊥ BD nên ⊥ (SAC),

⇒ BD ⊥ SA mà DF ⊥ SA nên SA ⊥ (BDF),

⇒ SA ⊥ BF.

Vì SA ⊥ BF và DF ⊥ SA nên [D, SA, B] = 

⇒ B, D sai.