Bài 3 trang 22 Toán 8 Tập 2 Chân trời sáng tạo

Bài 3 trang 22 Toán 8 Tập 2 Chân trời sáng tạo: 

a) Vẽ đồ thị các hàm số sau đây trên cùng một mặt phẳng tọa độ:

y = x; y = x +2; y = –x; y = –x + 2

b) Bốn đồ thị nói trên cắt nhau tại các điểm O(0;0), A, B, C. Tứ giác có 4 đỉnh O, A, B, C là hình gì? Giải thích.

Giải bài 3 trang 22 Toán 8 Tập 2 Chân trời sáng tạo:

a) Vẽ đồ thị các hàm số trên cùng một mặt phẳng tọa độ:

• Với hàm số y = x, cho x = 1 thì y = 1.

Đồ thị hàm số y = x đi qua các điểm O(0; 0) và C(1; 1).

• Với hàm số y = x + 2, cho x = 0 thì y = 2, cho x = −1 thì y = 1.

Đồ thị hàm số y = x + 2 đi qua các điểm B(0; 2) và A(−1; 1).

• Với hàm số y = −x, cho x = −1 thì y = 1.

Đồ thị hàm số y = −x đi qua các điểm O(0; 0) và A(−1; 1).

• Với hàm số y = −x + 2, cho x = 0 thì y = 2, cho x = 1 thì y = 1.

Đồ thị hàm số y = −x + 2 đi qua các điểm B (0; 2) và C(1; 1).

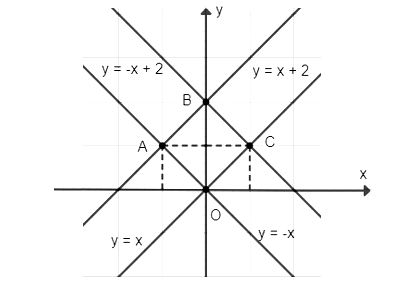
b) Tứ giác có 4 đỉnh O, A, B, C là hình gì? Giải thích.

Ta có:

Đường thẳng y = x song song với đường thẳng y = x + 2 suy ra OC // AB.

Đường thẳng y = −x song song với đường thẳng y = −x + 2 suy ra OA // BC.

Tứ giác OABC có: OC // AB, OA // BC

⇒ Tứ giác OABC là hình bình hành.

Hình bình hành OABC có hai đường chéo OB và AC vuông góc và bằng nhau

⇒ Tứ giác OABC là hình vuông.