Hệ phương trình đối xứng loại 2, Cách giải và Bài tập vận dụng - Toán lớp 10

09:10:5917/07/2021

Hệ phương trình đối xứng loại 2 theo ẩn x và y hiểu đơn giản là hệ phương trình mà khi ta đổi vai trò (vị trí) của hai ẩn x và y thì hai phương trình trong hệ sẽ hoán đổi cho nhau (nghĩa là pt(1) trở thành pt(2) và pt(2) trở thành pt(1)).

Vậy hệ phương trình đối xứng loại 2 có dạng như thế nào? cách giải hệ phương trình đối xứng loại 2 ra sao? chúng ta sẽ làm biết trong bài viết này và qua đó vận dụng giải minh họa một số bài tập về hệ phương trình đối xứng loại 2.

» Đừng bỏ lỡ: Cách giải hệ phương trình đẳng cấp bậc 2, bậc 3 cực hay

• Hệ phương trình đối xứng loại 2

- Hệ phương trình đối xứng loại 2 có dạng: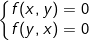 $\small \left\{\begin{matrix} f(x,y)=0\\ f(y,x)=0 \end{matrix}\right.$

* Ví dụ phương trình đối xứng loại 2: 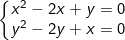$\small \left\{\begin{matrix} x^2-2x +y =0\\ y^2-2y+x=0 \end{matrix}\right.$

• Cách giải hệ phương trình đối xứng loại 2

+ Bước 1: Cộng hoặc trừ hai vế của hai phương trình trong hệ, ta thu được phương trình mới. Biến đổi phương trình này về phương trình tích, tìm biểu thức liên hệ giữa x và y đơn giản.

+ Bước 2: Thế x theo y (hoặc y theo x) vào một trong hai phương trình ban đầu của hệ.

+ Bước 3: Giải và tìm ra nghiệm x (hoặc y). Từ đó suy ra nghiệm còn lại.

+ Bước 4: Kết luận nghiệm của hệ phương trình.

• Bài tập về hệ phương trình đối xứng loại 2 có lời giải

* Bài tập 1: Giải hệ phương trình đối xứng loại 2 sau: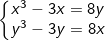 $\small \left\{\begin{matrix} x^3-3x=8y\\ y^3-3y=8x \end{matrix}\right.$

* Lời giải:

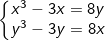
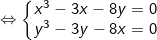
- ta có: $\small \left\{\begin{matrix} x^3-3x=8y\\ y^3-3y=8x \end{matrix}\right.$ $\small \Leftrightarrow \left\{\begin{matrix} x^3-3x-8y=0\\ y^3-3y-8x=0 \end{matrix}\right.$

lấy pt(1) trừ đi pt(2) ta được:

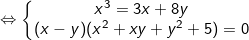
$\small \Leftrightarrow \left\{\begin{matrix} x^3=3x+8y\\ (x-y)(x^2+xy+y^2+5)=0 \end{matrix}\right.$

vì 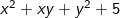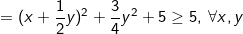$\small x^2+xy+y^2+5$ $\small =(x+\frac{1}{2}y)^2+\frac{3}{4}y^2+5\geq 5,\: \forall x,y$ nên hệ trên tương đương

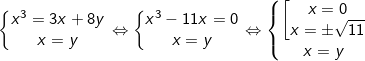
$\small \left\{\begin{matrix} x^3=3x+8y\\ x=y \end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x^3-11x=0\\ x=y \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \left \[\begin{matrix} x=0\\ x=\pm \sqrt{11} \end{matrix} \right.\\ x=y \end{matrix}\right.$

Vậy hệ có tập nghiệm: 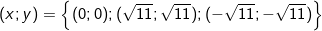$\small (x;y)= \left \{ (0;0);(\sqrt{11};\sqrt{11});(-\sqrt{11};-\sqrt{11}) \right \}$

* Bài tập 2: Giải hệ phương trình đối xứng loại 2 sau: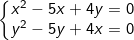 $\small \left\{\begin{matrix} x^2-5x+4y=0\\ y^2-5y+4x=0 \end{matrix}\right.$

* Lời giải:

- Trừ pt(1) (ở trên) cho pt(2) (ở dưới) của hệ ta được:

x² - y² -5x + 5y + 4y - 4x = 0

⇔ (x - y)(x + y) - 9(x - y) = 0

⇔ (x - y)(x + y - 9) = 0

⇔ x - y = 0 hoặc x + y - 9 = 0

+ TH1: Với x = y thay vào pt(1) ta được: y² - y = 0

⇔ y( y - 1) = 0 ⇔ y = 0 hoặc y = 1.

với y = 0 ⇒ x = 0;

với y = 1 ⇒ x = 1;

Hệ có nghiệm (x;y) ={(0;0; (1;1)}

+ TH2: Với x = 9 - y thay vào pt(2) được

y² - 5y +4(9 - y) = 0 (*)

⇔ y² - 9y + 36 = 0

Δ_y = (-9)² - 4.36 = 81 - 144 = -63<0 nên pt (*) này vô nghiệm.

- Kết luận cả 2 trường hợp: Hệ pt đã cho có nghiệm: (x;y) ={(0;0; (1;1)}

* Bài tập 3: Cho hệ phương trình đối xứng loại 2 theo tham số m sau:

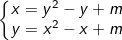
$\small \left\{\begin{matrix} x=y^2-y+m\\ y=x^2-x+m \end{matrix}\right.$

a) Tìm m để hệ phương trình đối xứng trên có nghiệm

b) Tìm m để hệ có nghiệm duy nhất

* Lời giải:

- Ta trừ pt(1) ở trên trừ cho pt(2) ở dưới được hệ mới:

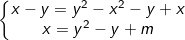
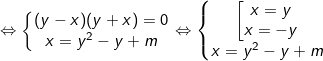
$\small \left\{\begin{matrix} x-y=y^2-x^2-y+x\\ x=y^2-y+m \end{matrix}\right.$ $\small \Leftrightarrow \left\{\begin{matrix} (y-x)(y+x)=0\\ x=y^2-y+m \end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \left \[\begin{matrix} x=y\\ x=-y \end{matrix} \right.\\ x=y^2-y+m \end{matrix}\right.$

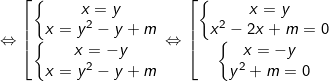
$\small \Leftrightarrow\left \[\begin{matrix} \left\{\begin{matrix} x=y\\ x=y^2-y+m \end{matrix}\right.\\ \left\{\begin{matrix} x=-y\\ x=y^2-y+m \end{matrix}\right. \end{matrix} \right. \Leftrightarrow\left \[\begin{matrix} \left\{\begin{matrix} x=y\\ x^2-2x+m=0 \end{matrix}\right.\\ \left\{\begin{matrix} x=-y\\ y^2+m=0 \end{matrix}\right. \end{matrix} \right.$

a) Hệ có nghiệm 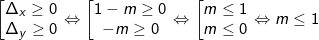$\small \left \[\begin{matrix} \Delta _x\geq 0\\ \Delta _y\geq 0 \end{matrix} \right.\Leftrightarrow \left \[\begin{matrix} 1-m\geq 0\\ -m\geq 0 \end{matrix} \right.\Leftrightarrow \left \[\begin{matrix} m\leq 1\\ m\leq 0 \end{matrix} \right.\Leftrightarrow m\leq 1$

Vậy m ≤ 1 thì hệ pt có nghiệm

b) Hệ có nghiệm duy nhất:

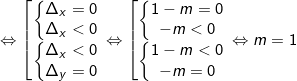
$\small \Leftrightarrow \left \[\begin{matrix} \left\{\begin{matrix} \Delta _x=0\\ \Delta _x<0 \end{matrix}\right.\\ \left\{\begin{matrix} \Delta _x<0\\ \Delta _y=0 \end{matrix}\right. \end{matrix} \right.\Leftrightarrow \left \[\begin{matrix} \left\{\begin{matrix} 1-m=0\\ -m<0 \end{matrix}\right.\\ \left\{\begin{matrix} 1-m<0\\ -m=0 \end{matrix}\right. \end{matrix} \right.\Leftrightarrow m=1$

Vậy m = 1 thì hệ pt có nghiệm duy nhất.

* Bài tập 4: Giải hệ phương trình đối xứng loại 2 sau: 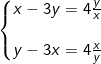$\small \left\{\begin{matrix} x-3y=4\frac{y}{x}\\ \\ y-3x=4\frac{x}{y} \end{matrix}\right.$

* Lời giải:

- Điều kiện:x ≠ 0, y ≠ 0

- Lấy pt(1) ở trên trừ pt(2) ở dưới ta được:

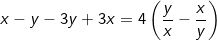
$\small x-y-3y+3x=4\left ( \frac{y}{x}-\frac{x}{y} \right )$

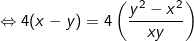
$\small \Leftrightarrow 4(x-y)=4\left ( \frac{y^2-x^2}{xy} \right )$

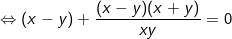
$\small \Leftrightarrow (x-y)+ \frac{(x-y)(x+y)}{xy}=0$

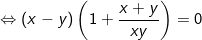
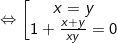
$\small \Leftrightarrow (x-y)\left (1+ \frac{x+y}{xy} \right )=0$ $\small \Leftrightarrow \left \[\begin{matrix} x=y\\ 1+\frac{x+y}{xy}=0 \end{matrix} \right.$

+ TH1: x - y = 0 thay vào pt(1) ta có: -2x = 4 ⇒ x = -2 = y (thỏa).

suy ra hệ có nghiệm là: (x;y) = (-2;-2).

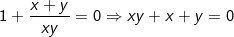
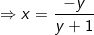
+ TH2: $\small 1+\frac{x+y}{xy}=0\Rightarrow xy+x+y=0$ $\small \Rightarrow x=\frac{-y}{y+1}$

Thay vào pt(1) ta được: 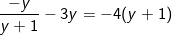$\small \frac{-y}{y+1}-3y=-4(y+1)$

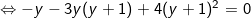
$\small \Leftrightarrow -y-3y(y+1)+4(y+1)^2=0$

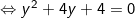
$\small \Leftrightarrow y^2+4y+4=0$

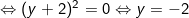
$\small \Leftrightarrow (y+2)^2=0\Leftrightarrow y=-2$

Với y = -2 ⇒ x = -2 (thỏa). Suy ra hệ có nghiệm (x;y) = (-2;-2)

- Kết luận: Cả 2 TH ta có nghiệm của hệ là (x;y) = (-2;-2).

* Bài tập 5: Giải hệ phương trình đối xứng sau: 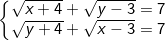$\small \left\{\begin{matrix} \sqrt{x+4} + \sqrt{y-3}= 7 \\ \sqrt{y+4} + \sqrt{x-3}= 7 \end{matrix}\right.$

* Lời giải:

- Điều kiện: x ≥ 3, y ≥ 3.

- Ta lấy pt(1) ở trên trừ đi pt(2) ở dưới, được:

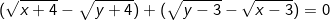
$\small (\sqrt{x+4}-\sqrt{y+4})+(\sqrt{y-3}-\sqrt{x-3})=0$

Nhân liên hợp cho mỗi nhóm ở trên (và để ý là x =3; y =3 không là nghiệm của hệ pt) ta được pt tương đương sau:

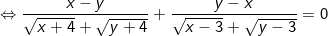
$\small \Leftrightarrow \frac{x-y}{\sqrt{x+4}+\sqrt{y+4}}+\frac{y-x}{\sqrt{x-3}+\sqrt{y-3}}=0$

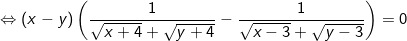
$\small \Leftrightarrow (x-y)\left ( \frac{1}{\sqrt{x+4}+\sqrt{y+4}} -\frac{1}{\sqrt{x-3}+\sqrt{y-3}}\right )=0$

+ TH1: x - y = 0 ⇒ x = y thay vào pt(1) được:

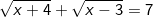$\small \sqrt{x+4}+\sqrt{x-3}=7$ [bình phương hai vế]

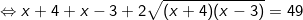
$\small \Leftrightarrow x+4+x-3+2\sqrt{(x+4)(x-3)}=49$

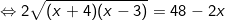
$\small \Leftrightarrow 2\sqrt{(x+4)(x-3)}=48-2x$

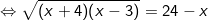$\small \Leftrightarrow \sqrt{(x+4)(x-3)}=24-x$ [bình phương hai vế, với x≤24]

$\small \Leftrightarrow (\sqrt{(x+4)(x-3)})^2=(24-x)^2$

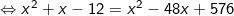
$\small \Leftrightarrow x^2+x-12=x^2-48x+576$

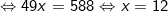$\small \Leftrightarrow 49x=588\Leftrightarrow x=12$ (thỏa)

Với x = 12 ⇒ y = 12

Vậy hệ có nghiệm là (x;y) = (12;12).

* Bài tập 6: Giải hệ phương trình đối xứng sau: 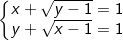$\small \left\{\begin{matrix} x+\sqrt{y-1}=1\\ y+\sqrt{x-1}=1 \end{matrix}\right.$

* Bài tập 7: Giải hệ phương trình đối xứng sau: 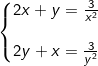$\small \left\{\begin{matrix} 2x+y=\frac{3}{x^2}\\ \\ 2y+x=\frac{3}{y^2} \end{matrix}\right.$

* Bài tập 8: Giải hệ phương trình đối xứng sau: 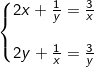$\small \left\{\begin{matrix} 2x+\frac{1}{y}=\frac{3}{x}\\ \\ 2y+\frac{1}{x}=\frac{3}{y} \end{matrix}\right.$

* Bài tập 9: Cho hệ phương trình đối xứng với tham số m sau: 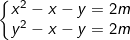$\small \left\{\begin{matrix} x^2-x-y=2m\\ y^2-x-y=2m \end{matrix}\right.$

a) Giải hệ với m = 0

b) Tìm m để hệ có nghiệm duy nhất

* Bài tập 10: Cho hệ phương trình đối xứng với tham số m sau: 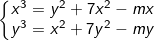$\small \left\{\begin{matrix} x^3=y^2+7x^2-mx\\ y^3=x^2+7y^2-my \end{matrix}\right.$

Tìm m để hệ pt đối xứng trên có nghiệm duy nhất.

Như vậy, với bài viết về Hệ phương trình đối xứng loại 2, Cách giải và Bài tập vận dụng ở trên, hy vọng các em đã hiểu rõ về phương trình đối xứng loại 2, nắm được cách giải qua các bài tập hướng dẫn từ đó có thể vận dụng tốt khi gặp các bài toán tương tự.

Hệ phương trình đối xứng loại 2, Cách giải và Bài tập vận dụng - Toán lớp 10

Tags:

Đánh giá & nhận xét