Bài 6.5 trang 9 Toán 10 tập 2 Kết nối tri thức
Bài 6.5 trang 9 SGK Toán 10 Tập 2 Kết nối tri thức là bài tập tổng hợp, yêu cầu vẽ đồ thị của hàm số bậc nhất và hàm số bậc hai, sau đó xác định các khoảng đồng biến (đi lên) và nghịch biến (đi xuống) của chúng.
Đề bài 6.5 trang 9 Toán 10 KNTT:
Vẽ đồ thị các hàm số sau và chỉ ra các khoảng đồng biến, nghịch biến của chúng.
a) y = – 2x + 1;
b) $y=-\frac{1}{2}x^2$
Phân tích và Hướng dẫn giải:
a) Hàm số $y = -2x + 1$
-
Đồ thị: Là đường thẳng, xác định bằng hai điểm.
-
Đơn điệu: Dựa vào hệ số góc $a$. Nếu $a < 0$, hàm số nghịch biến trên $\mathbb{R}$.
b) Hàm số $y = -\frac{1}{2}x^2$
-
Đồ thị: Là Parabol có đỉnh tại gốc tọa độ $O(0; 0)$.
-
Đơn điệu: Dựa vào dấu của $a$. Vì $a < 0$, Parabol quay bề lõm xuống dưới, nên hàm số đồng biến khi $x < 0$ và nghịch biến khi $x > 0$.
Lời giải chi tiết bài 6.5 trang 9 Toán 10:
a) y = – 2x + 1
Tập xác định của hàm số này là D = R
Với x = 0 thì y = 1, với x = 1 thì y = – 1.
Đồ thị hàm số y = – 2x + 1 là đường thẳng đi qua 2 điểm (0; 1) và (1; – 1).
Đồ thị có dạng như sau:
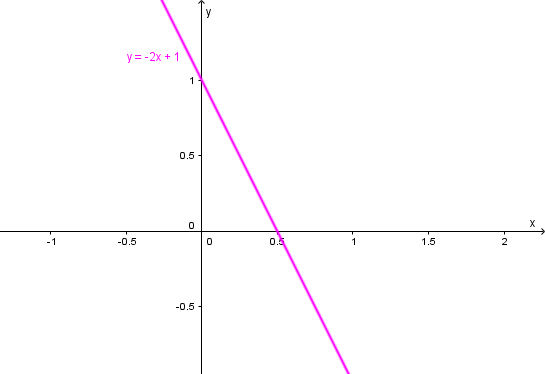
Ta thấy đồ thị hàm số đi xuống từ trái qua phải trên R nên hàm số nghịch biến trên R.
b)
Tập xác định của hàm số này là D = R
Bảng giá trị của x và y tương ứng:
|
x |
0 |
1 |
– 1 |
2 |
– 2 |
|
y |
0 |
– 1/2 | – 1/2 |
– 2 |
– 2 |
Đồ thị hàm số là đường cong đi qua các điểm (0; 0), , (2; – 2), (– 2; – 2).
Đồ thị có dạng như sau:
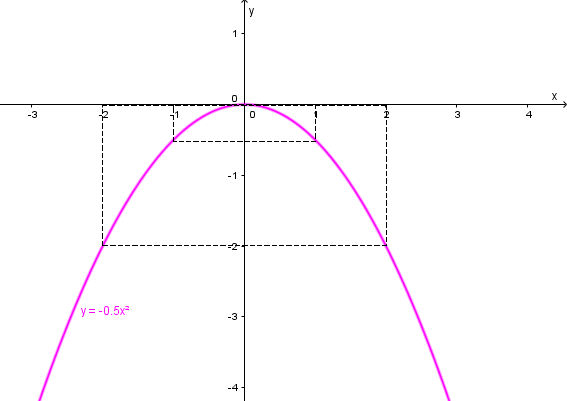
Ta thấy hàm số đi lên từ trái sang phải trên (– ∞; 0) và đi xuống từ trái sang phải trên (0; + ∞).
Vậy hàm số đồng biến trên khoảng (– ∞; 0) và nghịch biến trên khoảng (0; + ∞).
Tổng kết: Bài 6.5 trang 9 SGK Toán 10 Tập 2 Kết nối tri thức đã củng cố quy tắc xác định tính đơn điệu của hàm số từ hệ số $a$.
| Hàm số | Dạng | Khoảng Đồng biến | Khoảng Nghịch biến |
| a) $y = -2x + 1$ | Bậc nhất ($a < 0$) | Không có | $\mathbf{(-\infty; +\infty)}$ |
| b) $y = -\frac{1}{2}x^2$ | Bậc hai ($a < 0$) | $\mathbf{(-\infty; 0)}$ | $\mathbf{(0; +\infty)}$ |
Nắm vững cách xác định tính đơn điệu từ đồ thị là chìa khóa để giải quyết các bài toán về cực trị. Hãy thường xuyên ghé thăm hayhochoi.vn để cập nhật thêm nhiều bài giải và kiến thức toán học bổ ích khác nhé!
• Xem thêm:
Đánh giá & nhận xét
-
 Bài 16 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 16 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 15 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 15 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 14 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 14 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 13 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 13 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 12 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 12 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 11 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 11 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 10 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 10 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 9 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 9 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 8 trang 96 Toán 10 tập 2 Kết nối tri thức
Bài 8 trang 96 Toán 10 tập 2 Kết nối tri thức
-
 Bài 7 trang 95 Toán 10 tập 2 Kết nối tri thức
Bài 7 trang 95 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6 trang 95 Toán 10 tập 2 Kết nối tri thức
Bài 6 trang 95 Toán 10 tập 2 Kết nối tri thức
-
 Bài 5 trang 95 Toán 10 tập 2 Kết nối tri thức
Bài 5 trang 95 Toán 10 tập 2 Kết nối tri thức
-
 Bài 4 trang 95 Toán 10 tập 2 Kết nối tri thức
Bài 4 trang 95 Toán 10 tập 2 Kết nối tri thức
-
 Bài 3 trang 95 Toán 10 tập 2 Kết nối tri thức
Bài 3 trang 95 Toán 10 tập 2 Kết nối tri thức
-
 Bài 2 trang 95 Toán 10 tập 2 Kết nối tri thức
Bài 2 trang 95 Toán 10 tập 2 Kết nối tri thức
-
 Bài 1 trang 95 Toán 10 tập 2 Kết nối tri thức
Bài 1 trang 95 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.14 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.14 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.13 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.13 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.12 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.12 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.11 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.11 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.10 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.10 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.9 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.9 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.8 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.8 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.7 trang 16 Toán 10 tập 2 Kết nối tri thức
Bài 6.7 trang 16 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.6 trang 9 Toán 10 tập 2 Kết nối tri thức
Bài 6.6 trang 9 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.4 trang 9 Toán 10 tập 2 Kết nối tri thức
Bài 6.4 trang 9 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.3 trang 9 Toán 10 tập 2 Kết nối tri thức
Bài 6.3 trang 9 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.2 trang 9 Toán 10 tập 2 Kết nối tri thức
Bài 6.2 trang 9 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.1 trang 9 Toán 10 tập 2 Kết nối tri thức
Bài 6.1 trang 9 Toán 10 tập 2 Kết nối tri thức
-
 Bài 6.26 trang 28 Toán 10 tập 2 Kết nối tri thức: Tính đơn điệu hàm số bậc 2
Bài 6.26 trang 28 Toán 10 tập 2 Kết nối tri thức: Tính đơn điệu hàm số bậc 2
-
 Bài 6.19 trang 24 Toán 10 tập 2 Kết nối tri thức: Bất phương trình bậc 2
Bài 6.19 trang 24 Toán 10 tập 2 Kết nối tri thức: Bất phương trình bậc 2
-
 Bài 7.25 SGK Toán 10 tập 2 Kết nối tri thức
Bài 7.25 SGK Toán 10 tập 2 Kết nối tri thức
-
 Bài 9.22 SGK Toán 10 tập 2 Kết nối tri thức
Bài 9.22 SGK Toán 10 tập 2 Kết nối tri thức
-
 Bài 9.21 SGK Toán 10 tập 2 Kết nối tri thức
Bài 9.21 SGK Toán 10 tập 2 Kết nối tri thức
-
 Bài 9.20 SGK Toán 10 tập 2 Kết nối tri thức
Bài 9.20 SGK Toán 10 tập 2 Kết nối tri thức
-
 Bài 9.19 SGK Toán 10 tập 2 Kết nối tri thức
Bài 9.19 SGK Toán 10 tập 2 Kết nối tri thức
-
 Bài 9.18 SGK Toán 10 tập 2 Kết nối tri thức
Bài 9.18 SGK Toán 10 tập 2 Kết nối tri thức
-
 Bài 9.17 SGK Toán 10 tập 2 Kết nối tri thức
Bài 9.17 SGK Toán 10 tập 2 Kết nối tri thức
-
 Bài 9.16 SGK Toán 10 tập 2 Kết nối tri thức
Bài 9.16 SGK Toán 10 tập 2 Kết nối tri thức


















































