Bài 6.7 trang 16 Toán 10 tập 2 Kết nối tri thức

Bài 6.7 Toán 10 trang 16 Tập 2 Kết nối tri thức:

Vẽ các đường parabol sau: 

a) y = x² – 3x + 2; 

b) y = – 2x² + 2x + 3; 

c) y = x² + 2x + 1; 

d) y = – x² + x – 1.

Giải bài 6.7 Toán 10 trang 16 Tập 2 Kết nối tri thức:

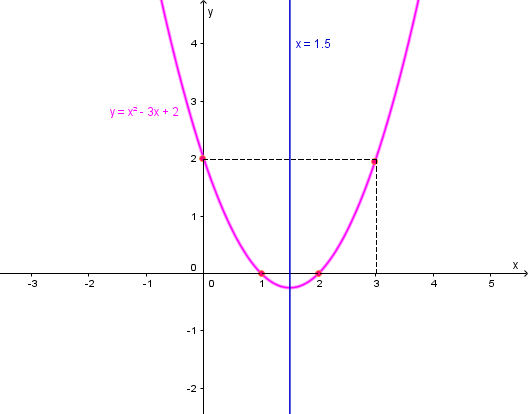
a) y = x² – 3x + 2 

Ta có: a = 1 > 0 nên parabol quay bề lõm lên trên. 

Parabol y = x² – 3x + 2 có: 

+ Tọa độ đỉnh 

+ Trục đối xứng 

+ Giao điểm của đồ thị với trục Oy là A(0; 2). 

+ Parabol cắt trục hoành tại hai điểm có hoành độ là nghiệm của phương trình x² – 3x + 2 = 0, tức là x = 2 và x = 1; 

+ Điểm đối xứng với điểm A qua trục đối xứng  là B(3; 2). 

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ.

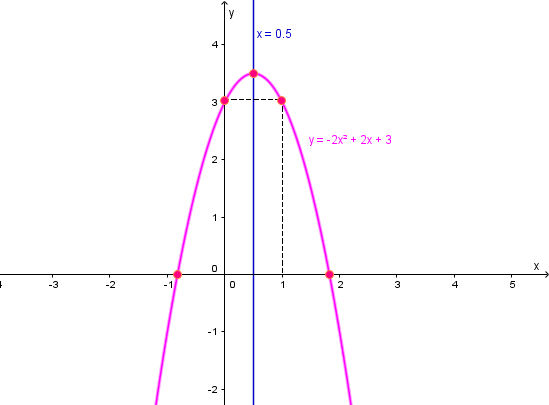
b) y = – 2x² + 2x + 3 

Ta có: a = – 2 < 0 nên parabol quay bề lõm xuống dưới. 

Parabol y = – 2x² + 2x + 3 có: 

+ Tọa độ đỉnh 

+ Trục đối xứng 

+ Giao điểm của đồ thị với trục Oy là A(0; 3). 

+ Parabol cắt trục hoành tại hai điểm có hoành độ là nghiệm của phương trình – 2x² + 2x + 3 = 0, tức là  và 

+ Điểm đối xứng với điểm A qua trục đối xứng  là B(1; 3). 

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ:

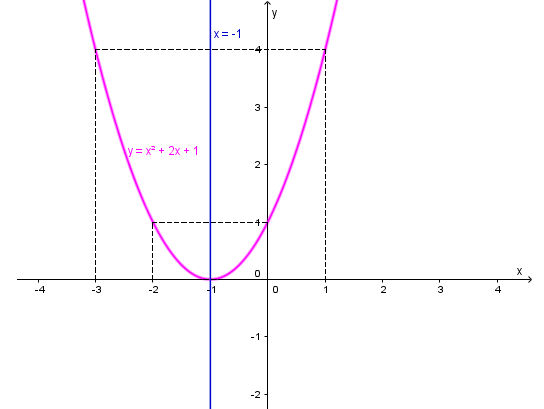
c) y = x² + 2x + 1 

Ta có: a = 1 > 0 nên parabol quay bề lõm lên trên. 

Parabol y = x² + 2x + 1 có: 

+ Tọa độ đỉnh I(– 1; 0)

+ Trục đối xứng x = – 1;

+ Giao điểm của đồ thị với trục Oy là A(0; 1). 

+ Điểm đối xứng với điểm A qua trục đối xứng x = – 1 là B(– 2; 1). 

+ Lấy điểm C(1; 4) thuộc parabol, điểm đối xứng với C qua trục đối xứng x = – 1 là D(– 3; 4).

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ:

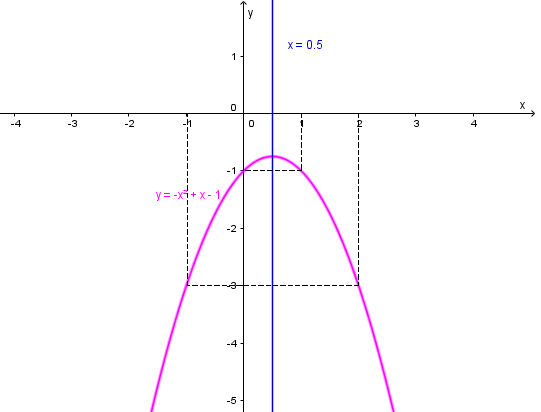
d) y = – x² + x – 1

Ta có: a = – 1 < 0 nên parabol quay bề lõm xuống dưới. 

Parabol y = – x² + x – 1 có: 

+ Tọa độ đỉnh 

+ Trục đối xứng 

+ Giao điểm của đồ thị với trục Oy là A(0; – 1). 

+ Điểm đối xứng với điểm A qua trục đối xứng  là B(1; – 1). 

+ Lấy điểm C(2; – 3) thuộc parabol, điểm đối xứng  với trục đối xứng là D(– 1; – 3). 

Vẽ đường cong đi qua các điểm trên ta được parabol cần vẽ.