Bài 6.14 trang 16 Toán 10 tập 2 Kết nối tri thức

Đề bài 6.14 trang 16 Toán 10 KNTT:

Quỹ đạo của một vật được ném lên từ gốc O (được chọn là điểm ném) trong mặt phẳng tọa độ Oxy là một parabol có phương trình  trong đó x (mét) là khoảng cách theo phương ngang trên mặt đất từ vị trí của vật đến gốc O, y (mét) là độ cao của vậy so với mặt đất (H.6.15). 

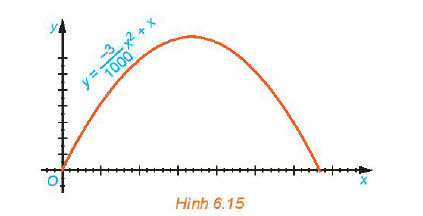
a) Tìm độ cao lớn nhất của vật trong quá trình bay. 

b) Tính khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O. Khoảng cách này gọi là tầm xa của quỹ đạo. 

Phân tích và Hướng dẫn giải:

Hàm số quỹ đạo là $y = -\frac{3}{1000}x^2 + x$.

1. Độ cao lớn nhất (Câu a): Hàm số đạt Giá trị lớn nhất tại đỉnh Parabol. Độ cao lớn nhất chính là tung độ đỉnh $y_I$.

2. Tầm xa (Câu b): Vật chạm đất khi độ cao $y = 0$. Ta giải phương trình $y = 0$ để tìm hoành độ $x$ (tầm xa).

Lời giải chi tiết bài 6.14 trang 16 Toán 10:

a) Độ cao lớn nhất của vật trong quá trình bay chính là tung độ đỉnh của parabol có phương trình:

$y=\frac{-3}{1000}x^2+x$

Ta có tọa độ đỉnh là $I\left ( \frac{500}{3};\frac{250}{3} \right )$

Vậy độ cao lớn nhất của vật trong quá trình bay là: $\frac{250}{3}\approx 83,33\: (m)$

b) Khi vật chạm đất, tức là y = 0 hay

$\frac{-3}{1000}x^2+x=0$

$\Leftrightarrow x\left (\frac{-3}{1000}x+1 \right )=0$

$\Leftrightarrow \left \[\begin{matrix} x=0\\ x=\frac{1000}{3} \end{matrix} \right.$

Ta loại x = 0 vì đây là vị trí điểm gốc tọa độ O. 

Vậy khoảng cách từ điểm chạm đất sau khi bay của vật đến gốc O hay tầm xa của quỹ đạo là 1000/3 ≈ 333,3 mét.