Giải bài 4 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo

Đề bài 4 trang 17 Toán 10 CTST:

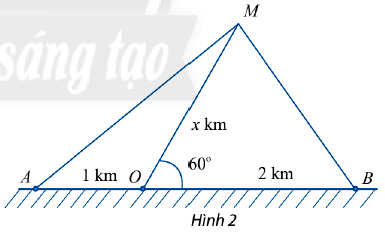
Một con tàu biển M rời cảng O và chuyển động thẳng theo phương tạo với bờ biển một góc 60°. Trên bờ biển có hai đài quan sát A và B nằm về hai phía so với cảng O và lần lượt cách cảng O khoảng cách 1km và 2km (Hình 2).

a) Đặt độ dài của MO là x km. Biểu diễn khoảng cách từ tàu đến A và từ tàu đến B theo x.

b) Tìm x để khoảng cách từ tàu đến B bằng 4/5 khoảng cách từ tàu đến A.

c) Tìm x để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O đúng 500m.

Lưu ý: Làm tròn kết quả đến hàng phần trăm.

Phân tích và Hướng dẫn giải:

1. Thiết lập góc: Góc $\angle MOB = 60^\circ$. Vì $A$ và $B$ nằm về hai phía so với $O$, góc $\angle MOA = 180^\circ - 60^\circ = 120^\circ$.

2. Định lý Côsin: Áp dụng cho $\triangle MOB$ và $\triangle MOA$ để tìm $MB$ và $MA$.

   $\mathbf{c^2 = a^2 + b^2 - 2ab \cos C}$

3. Lập phương trình: Chuyển các điều kiện về khoảng cách thành phương trình chứa căn và giải.

Lời giải chi tiết bài 4 trang 17 Toán 10:

a) Xét tam giác MOB:

Áp dụng định lí côsin, ta có:

MB² = OM² + OB² – 2.OM.OB.cos

⇔ MB² = x² + 2² – 2.x.2.cos60°

⇔ MB² = x² + 4 – 2x

Ta lại có: 

Xét tam giác MOA có:

Áp dụng định lí côsin, ta có:

MA² = OM² + OA² – 2.OM.OA.cos

⇔ MA² = x² + 1² – 2.x.1.cos120°

⇔ MA² = x² + 1 + x

Vậy có:

$MA=\sqrt{x^2+x+1}\: (km)$ và $MB=\sqrt{x^2-2x+4}\: (km)$

b) Để khoảng cách từ tàu đến B bằng 4/5 khoảng cách từ tàu đến A thì

$\sqrt{x^2-2x+4}=\frac{4}{5}\sqrt{x^2+x+1}$

⇒ x² – 2x + 4 = (16/25)(x² + x + 1)

⇒ 25x² – 50x + 100 = 16x² + 16x + 16

⇒ 9x² – 66x + 84 = 0

Suy ra: hoặc 

Thay lần lượt các giá trị trên vào phương trình đã cho ta thấy cả hai giá trị đều thỏa mãn.

Vậy với  hoặc  thì khoảng cách từ tàu đến B bằng 4/5 khoảng cách từ tàu đến A.

c) Đổi 500 m = 0,5 km = 1/2 (km)

Để khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O 500 m thì

$\sqrt{x^2-2x+4}=x-\frac{1}{2}$

⇔ x² – 2x + 4 = x² – x + 1/4

⇔ –x = -15/4

⇔ x = 15/4

Vậy x = 15/4 thì khoảng cách từ tàu đến B nhỏ hơn khoảng cách từ tàu đến O là 500 m.