Giải bài 1 trang 12 Toán 10 Tập 2 SGK Chân trời sáng tạo
Bài 1 trang 12 SGK Toán 10 Tập 2 Chân trời sáng tạo yêu cầu học sinh sử dụng đồ thị hàm số bậc hai (y = f(x)) để xác định các khoảng giá trị của x thỏa mãn bất phương trình bậc hai tương ứng (f(x) > 0, f(x) < 0, f(x) ≥ 0, f(x) ≤ 0).
Đề bài 1 trang 12 Toán 10 CTST:
Dựa vào đồ thị của hàm số bậc hai tương ứng, hãy xác định tập nghiệm của các bất phương trình bậc hai sau đây:
Phân tích và Hướng dẫn giải:
Để tìm tập nghiệm của bất phương trình bậc hai $f(x) \diamondsuit 0$ từ đồ thị, ta dựa vào:
-
Nghiệm: Các hoành độ giao điểm của Parabol với trục $Ox$ ($f(x) = 0$).
-
Dấu của $f(x)$:
-
$f(x) > 0$: Khoảng Parabol nằm trên trục $Ox$.
-
$f(x) < 0$: Khoảng Parabol nằm dưới trục $Ox$.
-
Ta sẽ xét từng bất phương trình dựa trên thông tin đồ thị đã cho.
Lời giải chi tiết bài 10 trang 12 Toán 10:
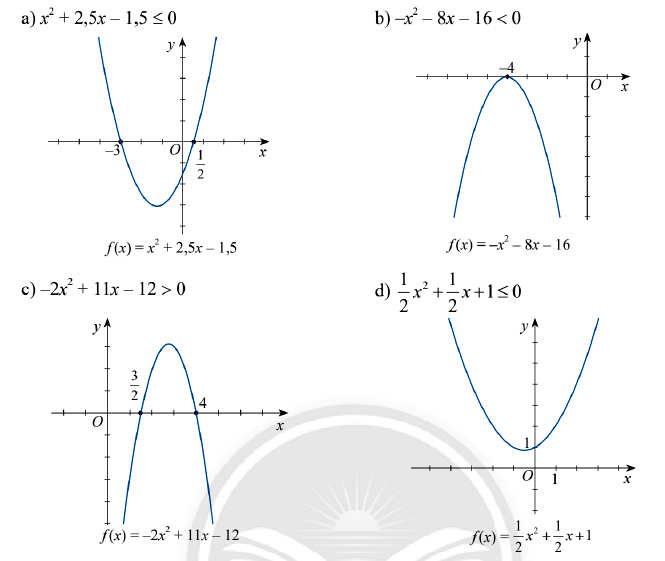
Dựa vào hình vẽ ta thấy:
Đồ thị hàm số f(x) cắt trục hoành tại hai điểm có hoành độ lần lượt là x1 = -3 và x2 = 1/2 hay với x1 = -3 và x2 = 1/2 thì f(x) = 0.
Trong hai khoảng (-∞; -3) và (1/2;+∞) đồ thị hàm số f(x) nằm phía trên trục hoành tức là f(x) > 0 khi x thuộc hai khoảng (-∞; -3) và (1/2;+∞).
Trong khoảng (-3; 1/2) đồ thị hàm số f(x) nằm phía dưới trục hoành, tức là là f(x) < 0 khi x thuộc khoảng (-3; 1/2).
Kết luận: Bất phương trình x2 + 2,5x – 1,5 ≤ 0 có tập nghiệm là S [-3; 1/2]
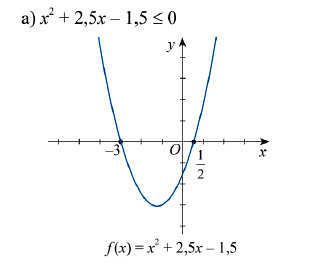
Dựa vào hình vẽ ta thấy:
Đồ thị hàm số f(x) cắt trục hoành tại một điểm có hoành độ x = -4 hay f(x) = 0 khi x = -4.
Với x ≠ -4 thì đồ thị hàm số f(x) nằm phía dưới trục hoành nên f(x) < 0 với x ≠ -4.
Kết luận: Bất phương trình – x2 – 8x – 16 < 0 có tập nghiệm là S = R\{-4}.
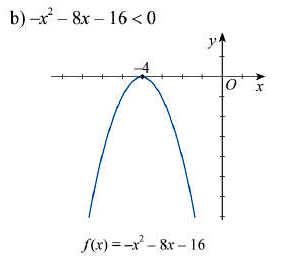
Dựa vào hình vẽ ta thấy:
Đồ thị hàm số cắt trục hoành tại hai điểm phân biệt có hoành độ lần lượt x1 = 3/2 và x2 = 4 hay f(x) = 0 khi x1 = 3/2 và x2 = 4.
Đồ thị hàm số f(x) nằm phía dưới trục hoành với x thuộc hai khoảng (-∞; 3/2) và (4; +∞) hay f(x) < 0 với x ∈ (-∞; 3/2) ∪ (4; +∞).
Đồ thị hàm số f(x) nằm phía trên trục hoành với x thuộc khoảng (3/2; 4) hay f(x) > 0 với x thuộc khoảng (3/2; 4).
Kết luận: Bất phương trình – 2x2 + 11x – 12 > 0 có tập nghiệm S = (3/2; 4).
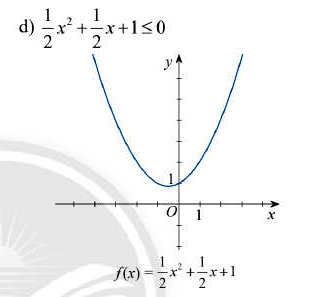
Dựa vào hình vẽ ta thấy:
Đồ thi hàm số f(x) nằm phía trên trục hoành với mọi x hay f(x) > 0 với x ∈ R.
Vậy bất phương trình ½x2 + ½x + 1 ≤ 0 có tập nghiệm S = Φ.
Bài 1 trang 12 SGK Toán 10 Tập 2 Chân trời sáng tạo đã củng cố cách tìm tập nghiệm bất phương trình bậc hai dựa trên phân tích đồ thị.
| Bất phương trình | Nghiệm (Gốc) | Dấu a | Tập nghiệm S |
| $x^2$ $+ 2,5x$ $– 1,5 \le 0$ | $-3, \frac{1}{2}$ | $a > 0$ | $\mathbf{\left[-3; \frac{1}{2}\right]}$ |
| $- x^2$ $– 8x$ $– 16 < 0$ | $-4$ (kép) | $a < 0$ | $\mathbf{\mathbb{R} \setminus \{-4\}}$ |
| $- 2x^2$ $+ 11x$ $– 12 > 0$ | $\frac{3}{2}, 4$ | $a < 0$ | $\mathbf{\left(\frac{3}{2}; 4\right)}$ |
| $\frac{1}{2}x^2$ $+ \frac{1}{2}x$ $+ 1 \le 0$ | Vô nghiệm | $a > 0$ | $\mathbf{\emptyset}$ |
Nắm vững mối quan hệ giữa dấu của $f(x)$ và vị trí Parabol so với trục hoành là chìa khóa để giải quyết các bài toán bất phương trình bậc hai. Hãy thường xuyên ghé thăm hayhochoi.vn để cập nhật thêm nhiều bài giải và kiến thức toán học bổ ích khác nhé!
• Xem thêm:
Đánh giá & nhận xét
-
 Giải bài 7 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 6 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 8 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 7 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 6 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải Bài tập Toán 10 tập 2 SGK Chân trời sáng tạo
Giải Bài tập Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 15 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 15 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 14 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 14 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 13 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 13 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 12 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 12 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 11 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 11 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 10 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 10 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 9 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 9 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 8 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 7 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 6 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo


















































