Giải bài 6 trang 71 Toán 10 tập 2 SGK Chân trời sáng tạo
Một cái cầu có dây cáp treo hình parabol, cầu dài 100m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống...
Bài 6 trang 71 Toán 10 tập 2 SGK Chân trời sáng tạo: Một cái cầu có dây cáp treo hình parabol, cầu dài 100m và được nâng đỡ bởi những thanh thẳng đứng treo từ cáp xuống, thanh dài nhất là 30m, thanh ngắn nhất là 6m (Hình 18). Tính chiều dài của thanh cách điểm giữa cầu 18m.
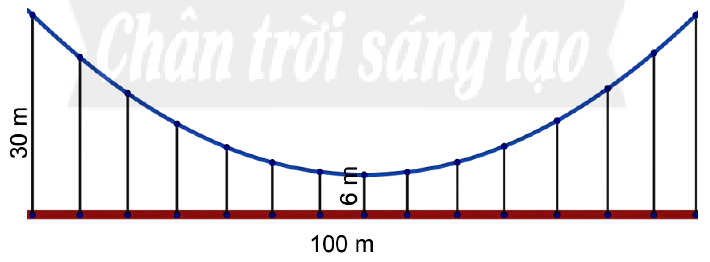
Giải bài 6 trang 71 Toán 10 tập 2 SGK Chân trời sáng tạo:
Chọn hệ tọa độ Oxy với gốc tọa độ tại điểm trên của thanh ngắn giữa cầu, trục tung tương ứng là mặt đường của cầu, vẽ lại hình như dưới đây:
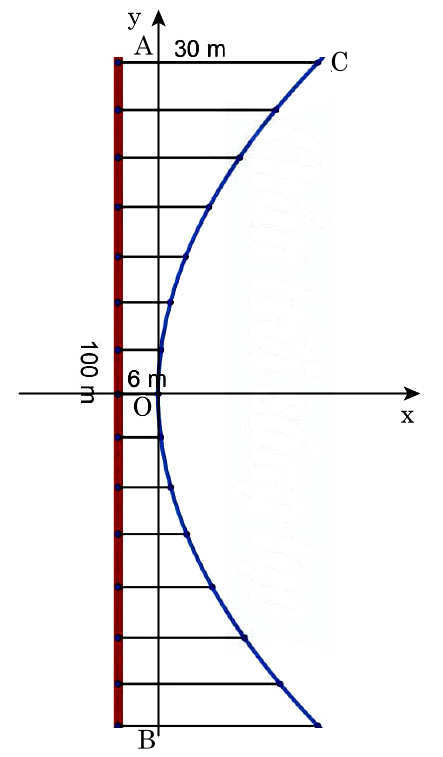
Ta nhận thấy cầu có dạng parabol nên gọi phương trình mô tả hình dạng cầu là y2 = 2px.
Cầu dài 100m tương ứng AB = 2OA = 100 ⇒ OA = 50, thanh dài nhất dài 30 m và thanh ngắn nhất là 6m
Nên suy ra AC = 30 - 6 = 24 (độ dài thanh dài nhất trừ đi độ dài thanh ngắn nhất)
Suy ra toạ độ điểm C trong hệ trục Oxy là: C(24;50)
Thay điểm C(24; 50) vào phương trình parabol trên ta được: 502 = 2p.24
Khi đó phương trình parabol là:
Gọi D là điểm nằm trên parabol cách điểm giữa cầu 18m, nghĩa là D(xD; 18).
Thay tọa độ điểm D vào parabol ta được:
Vậy chiều dài của thanh cách điểm giữa cầu 18m là: 3,11 + 6 = 9,11 (m).
Hy vọng với lời giải bài 6 trang 71 Toán 10 Tập 2 SGK Chân trời Sáng tạo ở trên đã giúp các em hiểu và nắm vững phần kiến thức này. Mọi góp ý và thắc mắc các em hãy để lại nhận xét dưới bài viết để Hay Học Hỏi ghi nhận và hỗ trợ, chúc các em học tốt.
• Xem giải bài tập Toán 10 SGK tập 2 Chân trời sáng tạo cùng chuyên mục
> Bài 1 trang 70 Toán 10 tập 2 SGK Chân trời sáng tạo: Viết phương trình chính tắc của:...
Đánh giá & nhận xét
-
 Giải bài 7 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 6 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 12 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 12 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 8 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 7 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 6 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải Bài tập Toán 10 tập 2 SGK Chân trời sáng tạo
Giải Bài tập Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 15 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 15 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 14 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 14 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 13 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 13 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 12 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 12 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 11 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 11 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 10 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 10 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 9 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 9 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 8 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 7 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo


















































