Giải bài 6 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Bài 6 trang 32 SGK Toán 10 Tập 2 Chân trời sáng tạo là bài toán hình học tổ hợp, yêu cầu tính số lượng hình bình hành được tạo thành từ giao điểm của hai nhóm đường thẳng song song khác nhau. Ta sử dụng kết hợp Tổ hợp (Cnk) và Quy tắc nhân.
Đề bài 6 trang 32 Toán 10 CTST:
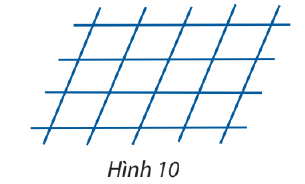
Có 4 đường thẳng song song cắt 5 đường thẳng song song khác tạo thành những hình bình hành (như Hình 10). Có bao nhiêu hình bình hành được tạo thành?
Phân tích và Hướng dẫn giải:
-
Định nghĩa Hình bình hành: Một hình bình hành được tạo thành bởi hai cặp đường thẳng song song.
-
Cặp thứ nhất (chiều rộng) được chọn từ nhóm $n_1 = 4$ đường thẳng song song.
-
Cặp thứ hai (chiều dài) được chọn từ nhóm $n_2 = 5$ đường thẳng song song khác.
-
-
Quy tắc đếm: Việc chọn hai đường thẳng để tạo thành một cặp là Tổ hợp chập 2 (vì thứ tự chọn không quan trọng).
-
Số cách chọn 2 đường từ nhóm 4: $C_4^2$.
-
Số cách chọn 2 đường từ nhóm 5: $C_5^2$.
-
-
Quy tắc nhân: Tổng số hình bình hành là tích của số cách chọn ở hai nhóm.
Lời giải chi tiết bài 6 trang 32 Toán 10:
Mỗi hình bình hành được tạo bởi 2 cặp đường thẳng song song. Việc tạo hình bình hành từ 4 đường thẳng song song cắt 5 đường thẳng song song khác được chia làm hai giai đoạn:
- Giai đoạn 1: Chọn một cặp đường thẳng song song từ 4 đường thẳng song song là tổ hợp chập 4 của 2, do đó có:
$C_{4}^{2}=\frac{4!}{(4-2)!.2!}$ $=\frac{4!}{2!2!}=\frac{4.3}{2.1}=6$ (cách).
- Giai đoạn 2: Ứng với cặp đường thẳng vừa chọn, chọn cặp đường thẳng song song từ 5 đường thẳng song song khác là tổ hợp chập 2 của 5, do đó có:
$C_{5}^{2}=\frac{5!}{(5-2)!.2!}$ $=\frac{5!}{3!2!}=\frac{5.4}{2.1}=10$(cách).
Theo quy tắc nhân ta có: (cách).
Vậy có tất cả 60 hình bình hành được tạo thành.
Tổng kết: Bài 6 trang 32 SGK Toán 10 Tập 2 Chân trời sáng tạo đã ứng dụng Tổ hợp ($C_n^k$) để giải bài toán đếm hình học.
-
Số hình bình hành là tích của số cách chọn các cặp cạnh song song.
-
Số cách chọn từ nhóm 4 đường: $\mathbf{C_4^2 = 6}$.
-
Số cách chọn từ nhóm 5 đường: $\mathbf{C_5^2 = 10}$.
-
Tổng số hình bình hành là $\mathbf{6 \cdot 10 = 60}$ hình.
Nắm vững việc nhận dạng cặp cạnh song song và áp dụng Tổ hợp là chìa khóa để giải quyết bài toán đếm hình học. Hãy thường xuyên ghé thăm hayhochoi.vn để cập nhật thêm nhiều bài giải và kiến thức toán học bổ ích khác nhé!
• Xem thêm:
Đánh giá & nhận xét
-
 Giải bài 7 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 32 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 25 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 24 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 17 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 13 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 12 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 12 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 8 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 7 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 6 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 5 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 4 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 3 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 2 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
Giải bài 1 trang 9 Toán 10 Tập 2 SGK Chân trời sáng tạo
-
 Giải Bài tập Toán 10 tập 2 SGK Chân trời sáng tạo
Giải Bài tập Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 15 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 15 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 14 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 14 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 13 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 13 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 12 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 12 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 11 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 11 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 10 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 10 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 9 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 9 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 8 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 7 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 7 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo
Giải bài 6 trang 74 Toán 10 tập 2 SGK Chân trời sáng tạo


















































