Giải bài 3 trang 10 Toán 10 Tập 2 SGK Chân trời sáng tạo

Đề bài 3 trang 10 Toán 10 CTST:

Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.

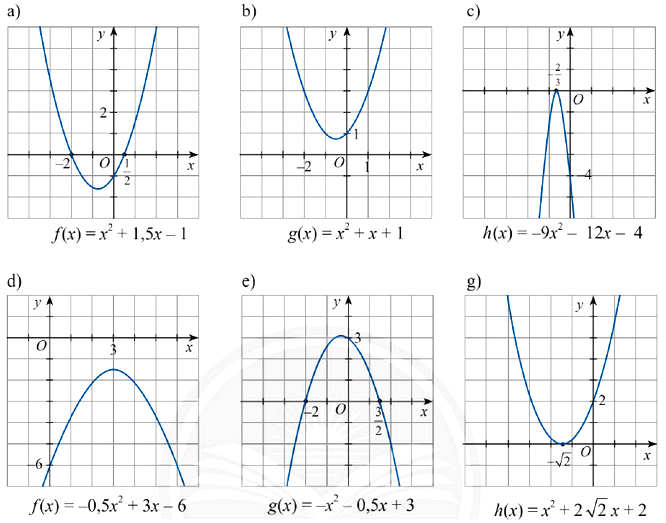
Phân tích và Hướng dẫn giải:

Để lập bảng xét dấu từ đồ thị, ta dựa vào mối quan hệ giữa đồ thị và trục hoành ($Ox$):

1. Nghiệm ($f(x) = 0$): Là các hoành độ giao điểm của đồ thị với trục $Ox$.

2. Dấu $f(x) > 0$: Khoảng $x$ mà đồ thị nằm phía trên trục $Ox$.

3. Dấu $f(x) < 0$: Khoảng $x$ mà đồ thị nằm phía dưới trục $Ox$.

Ta sẽ lập bảng xét dấu cho từng tam thức dựa trên thông tin đã cho.

Như vậy các bước giải như sau:

+ Bước 1: Xác định nghiệm của tam thức (là giao điểm của đồ thị với trục hoành)

+ Bước 2: Xác định khoảng mà f(x)>0 (khoảng đồ thị nằm trên trục hoành)

+ Bước 3: Xác định khoảng mà f(x)<0 (khoảng đồ thị nằm dưới trục hoành)

+ Bước 4: Lập bảng xét dấu

Lời giải chi tiết bài 3 trang 10 Toán 10:

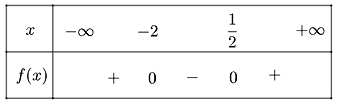
a) Tam thức f(x) = x² + 1,5x - 1

Có 2 nghiệm phân biệt là x₁ = - 2 và x₂ = 1/2

f(x) > 0 khi x ∈ (-∞, -2) U (1/2; +∞)

f(x) < 0 khi x ∈ (-2, 1/2)

Vậy ta có bảng xét dấu như sau:

b) Tam thức g(x) = x² + x + 1

 Vô nghiệm, g(x) > 0, ∀x∈R 

Ta có bảng xét dấu như sau: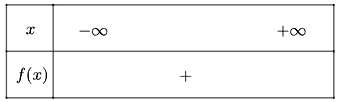

c) Tam thức h(x) = -9x² - 12x - 4 

Có nghiệm kép x₁ =  x₂ = -2/3 và h(x) < 0 ∀x ≠ -2/3

Ta có bảng xét dấu như sau:

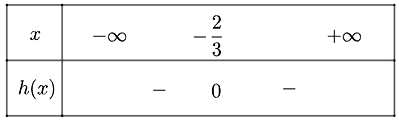
d) Tam thức f(x) = -0,5x² + 3x - 6

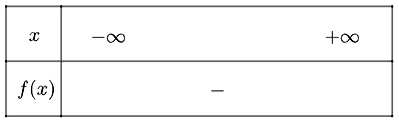
Vô nghiệm và f(x) < 0, ∀x∈R 

Ta có bảng xét dấu như sau:

e) Tam thức g(x) = -x² - 0,5x + 3

Có hai nghiệm x₁ = -2, x₂ = 3/2

g(x) > 0 khi x ∈ (-2; 3/2) và g(x) < 0 khi x ∈ (-∞, -2) U (3/2, +∞)

Ta có bảng xét dấu như sau:

g)  Tam thức h(x) = x²  + (2√2)x + 2

Có nghiệm kép x₁ = x₂ = -√2

h(x) > 0 với mọi x ≠ -√2.

Ta có bảng xét dấu như sau: