Hệ phương trình đối xứng loại 1, Cách giải và Bài tập vận dụng - Toán lớp 10
Hệ phương trình đối xứng loại 1 theo ẩn x và y hiểu đơn giản là hệ phương trình mà khi ta đổi vai trò (vị trí) của hai ẩn x và y thì hệ phương trình vẫn không thay đổi.
Vậy hệ phương trình đối xứng loại 1 có dạng như thế nào? cách giải hệ phương trình đối xứng loại 1 ra sao? chúng ta sẽ làm biết trong bài viết này và qua đó vận dụng giải minh họa một số bài tập về hệ phương trình đối xứng loại 1.
» Đừng bỏ lỡ: Cách giải Bài tập hệ phương trình đối xứng loại 2 cực hay
• Hệ phương trình đối xứng loại 1
- Hệ phương trình đối xứng loại 1 có dạng: 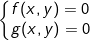 trong đó
trong đó 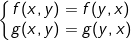
* Ví dụ: Hệ phương trình đối xứng loại 1: 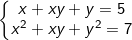
• Định lý Vi-ét cho phương trình bậc 2
- Nếu phương trình bậc hai ax2 + bx + c = 0 có 2 nghiệm phân biệt x1, x2 thì
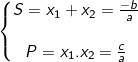
- Ngược lại, nếu hai số x1, x2 có: 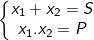 thì x1, x2 là nghiệm của phương trình:
thì x1, x2 là nghiệm của phương trình:
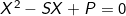

• Cách giải hệ phương trình đối xứng loại 1
+ Bước 1: Biểu diễn từng phương trình của hệ qua x+y và xy.
+ Bước 2: Đặt S = x + y, P = xy. Điều kiện hệ có nghiệm là S2 ≥ 4P. Ta được hệ mới chứa ẩn S và P.
+ Bước 3: Giải hệ phương trình với ẩn S, P để tìm ra S và P (sử dụng phương pháp thế hoặc cộng đại số).
+ Bước 4: Tìm được S và P, khi đó x và y là nghiệm của phương trình bậc hai:
X2 - SX + P = 0
+ Bước 5: Kết luận nghiệm của hệ phương trình.
* Lưu ý: Vì hệ phương trình là đối xứng nên nếu (x0;y0) là nghiệm của hệ thì (y0;x0) cũng là nghiệm của hệ phương trình.
• Bài tập về hệ phương trình đối xứng loại 1 có lời giải
* Bài tập 1: Giải hệ phương trình đối xứng loại 1 sau: 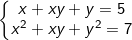 (I)
(I)
* Lời giải:
- Ta có: 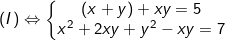
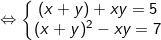
Đặt S = x + y; P = xy điều kiện S2 ≥ 4P, ta được:
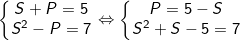
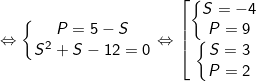
Mà S2 ≥ 4P nên ta thấy chỉ có S = 3, P = 2 thỏa mãn.
Khi đó: x, y là nghiệm của phương trình bậc hai: X2 - 3X + 2 = 0
⇔ (X - 1)(X - 2) = 0 ⇔ X = 1 hoặc X = 2.
Vậy hệ phương trình có nghiệm là (1;2), (2;1).
* Bài tập 2: Giải hệ phương trình đối xứng loại 1 sau: 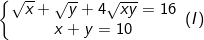
* Lời giải:
- Điều kiện: x≥0, y≥0;
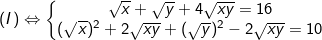
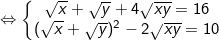
Đặt 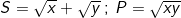
Điều kiện S≥0; P≥0 và S2 ≥ 4P. khi đó hệ (I) trở thành:
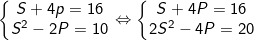
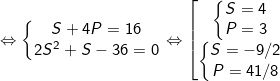
Ta thấy S, P ≥0 và S2 ≥ 4P nên chỉ có S = 4; P = 3 thỏa điều kiện.
Khi đó √x và √y là 2 nghiệm của phương trình: X2 - 4X + 3 = 0
⇔ (X - 1)(X - 3) = 0 ⇔ X = 1 hoặc X = 3.
- Trường hợp 1: 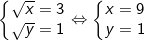
- Trường hợp 2: 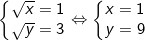
Ta thấy cả 2 cặp nghiệp đều thỏa mãn.
Vậy hệ phương trình có hai nghiệm: (x;y) = {(1;9); (9;1)}.
* Bài tập 3: Cho hệ phương trình đối xứng loại 1 có tham số m: 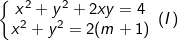
Tìm m để hệ phương trình đối xứng trên có đúng hai nghiệm.
* Lời giải:
- Ta có: 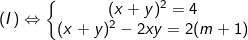
Đặt S = x + y; P = xy khi đó (I) trở thành:
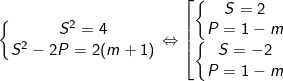
Khi đó (x;y) là nghiệm của phương trình bậc hai:
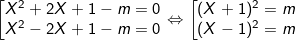
Như vậy để hệ có nghiệm duy nhât thì m = 0; khi đó 2 ngiệm của hệ là: (x;y) = {(1;1); (-1;-1)}.
* Bài tập 4: Giải hệ phương trình đối xứng loại 1: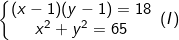
* Lời giải:
- Ta có: 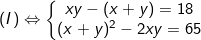
Đặt S = x + y; P = xy với điều kiện S2 ≥ 4P. Ta có hệ
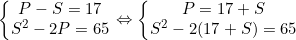
Từ: S2 - 2(17 + S) = 65
⇔ S2 - 2S - 99 = 0
⇔ (S + 9)(S - 11) = 0
⇔ S = -9 hoặc S = 11
+ Với S = -9 ⇒ P = 8 (thỏa), Khi đó x và y là nghiệm của phương trình bậc hai.
X2 + 9X + 8 = 0 ⇔ (X + 1)(X + 8) = 0 ⇔ X = -1 hoặc X = -8
⇒ hệ có 2 nghiệm là: (x;y) = {(-1;-8); (-8;-1)};
+ Với S = 11 ⇒ P = 28 (thỏa), Khi đó x và y là nghiệm của phương trình bậc hai.
X2 - 11X + 28 = 0 ⇔ (X - 4)(X - 7) = 0 ⇔ X = 4 hoặc X = 7
⇒ hệ có 2 nghiệm là: (x;y) = {(4;7); (7;4)};
- Kết luận: Vậy hệ phương trình có 4 nghiệm là: (x;y) = {(-1;-8); (-8;-1); (4;7); (7;4)}.
* Bài tập 5: Giải hệ phương trình đối xứng loại 1 sau: 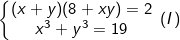
* Lời giải:
- Ta có: 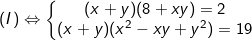
![\small \Leftrightarrow \left\{\begin{matrix} (x+y)(8+xy)=2\\ (x+y)[(x+y)^2-3xy]=19 \end{matrix}\right.](https://hayhochoi.vn/uploads/news/wyswyg/2021_07/1626344043up31vzfke8_1626422434.gif)
Đặt S = x + y; P = xy với điều kiện S2 ≥ 4P. Ta có hệ
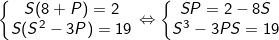
Ta thế: SP = 2 - 8S vào S3 - 3PS = 19 được:
S3 - 3(2 - 8S) = 19
⇔ S3 + 24S - 25 = 0 (nhẩm thấy có nghiệm S = 1) nên
⇔ (S - 1)(S2 + S + 25) = 0 ⇔ S = 1
(vì S2 + S + 25 = (S + 1/2)2 + 99/4 ≥ 99/4 với mọi S).
+ Với S = 1 ⇒ P = – 6 (thỏa), khi đó x và y là nghiệm của phương trình bậc hai.
X2 - X - 6 = 0 ⇔ (X + 2)(X - 3) = 0 ⇔ X = -2 hoặc X = 3.
Vậy hệ có 2 nghiệm là: (x;y) = {(3;-2); (-2;3)}.
* Bài tập 6: Giải các hệ phương trình đối xứng loại 1 sau:
a) 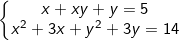
b) 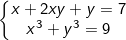
c) 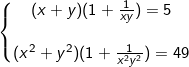
d) 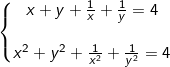
e) 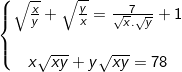
* Bài tập 7: Giải và biện luận hệ phương trình đối xứng loại 1 sau: 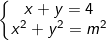
* Bài tập 8: Tìm m để hệ phương trình đối xứng loại 1 sau có nghiệm:
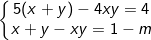
* Bài tập 9: Tìm m để hệ pt đối xứng loại 1 sau có nghiệm duy nhất:
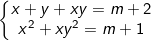
* Bài tập 10: Tìm m để hệ pt đối xứng loại 1 sau có đúng hai nghiệm:
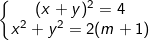
Như vậy, với bài viết về Hệ phương trình đối xứng loại 1, Cách giải và Bài tập vận dụng ở trên, hy vọng các em đã hiểu rõ về phương trình đối xứng loại 1, nắm được cách giải qua các bài tập hướng dẫn từ đó có thể vận dụng tốt khi gặp các bài toán tương tự.
Đánh giá & nhận xét
-
 Giải bài 9 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 9 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 8 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 8 trang 57 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 7 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 7 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 6 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 6 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 5 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 5 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 4 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 4 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 3 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 3 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 2 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 2 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 1 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 1 trang 56 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 7 trang 48 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 7 trang 48 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 6 trang 48 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 6 trang 48 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 5 trang 48 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 5 trang 48 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 4 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 4 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 3 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 3 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 2 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 2 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 1 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 1 trang 47 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 5 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 5 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 4 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 4 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 3 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 3 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 2 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 2 trang 38 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 1 trang 37 Toán 10 Chân trời sáng tạo (SGK Tập 1)
Giải bài 1 trang 37 Toán 10 Chân trời sáng tạo (SGK Tập 1)
-
 Giải bài 6 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 2 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 1 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo: Biểu diễn miền nghiệm
Giải bài 1 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo: Biểu diễn miền nghiệm
-
 Giải bài 10 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 10 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 9 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 9 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 8 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 8 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 7 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 7 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 6 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 6 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 5 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 5 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 4 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 4 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 3 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 2 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo: Mệnh đề
Giải bài 2 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo: Mệnh đề
-
 Giải bài 1 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
Giải bài 1 trang 27 Toán 10 tập 1 SGK Chân trời sáng tạo
-
 Giải bài 3.19 trang 45 Toán 10 Tập 1 SGK Kết nối tri thức
Giải bài 3.19 trang 45 Toán 10 Tập 1 SGK Kết nối tri thức
-
 Giải bài 3.18 trang 45 Toán 10 Tập 1 SGK Kết nối tri thức
Giải bài 3.18 trang 45 Toán 10 Tập 1 SGK Kết nối tri thức

















































