Giải bài 6 trang 39 Toán 10 tập 1 SGK Chân trời sáng tạo

Đề bài:

Một xưởng sản xuất có hai máy đặc chủng A, B sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng máy A trong 6 giờ và dùng máy B trong 2 giờ. Để sản xuất một tấn sản phẩm Y cần dùng máy A trong 2 giờ và dùng máy B trong 2 giờ. Cho biết mỗi máy không thể sản xuất đồng thời hai loại sản phẩm.

Máy A làm việc không quá 12 giờ một ngày; máy B làm việc không quá 8 giờ một ngày. Một tấn sản phẩm X lãi 10 triệu đồng và một tấn sản phẩm Y lãi 8 triệu đồng. Hãy lập kế hoạch sản xuất mỗi ngày sao cho tổng số tiền lãi cao nhất.

Phân tích và Hướng dẫn giải

Bài toán yêu cầu chúng ta tìm số lượng sản phẩm X và Y cần sản xuất để đạt được lợi nhuận lớn nhất, với hai điều kiện ràng buộc: thời gian làm việc của máy A và máy B.

Để giải bài toán này, chúng ta sẽ thực hiện các bước sau:

1. Lập hệ bất phương trình: Chúng ta sẽ gọi $x$ và $y$ là số tấn sản phẩm X và Y cần sản xuất. Dựa vào giới hạn thời gian của mỗi máy, chúng ta sẽ lập các bất phương trình tương ứng.

2. Xác định miền nghiệm: Chúng ta sẽ vẽ các đường thẳng trên mặt phẳng tọa độ để xác định vùng chứa tất cả các phương án sản xuất hợp lý. Vùng này chính là miền nghiệm của hệ bất phương trình.

3. Tìm biểu thức lợi nhuận: Xây dựng một biểu thức tính tổng số tiền lãi thu được theo $x$ và $y$.

4. Tính lợi nhuận tại các đỉnh: Miền nghiệm là một đa giác. Chúng ta sẽ tính giá trị của biểu thức lợi nhuận tại các đỉnh của đa giác này.

Lời giải chi tiết:

Gọi x (tấn) là khối lượng sản phẩm X mà xưởng sản xuất ra trong một ngày; y(tấn) là khối lượng sản phẩm Y mà xưởng sản xuất ra trong một ngày.

Hiển nhiên x ≥ 0 và y ≥ 0.

Để sản xuất x tấn sản phẩm X cần dùng máy A trong 6x (giờ) ; để sản xuất y tấn sản phẩm Y cần dùng máy A trong 2y (giờ).

Tổng số giờ dùng máy A trong một ngày là 6x + 2y (giờ).

Do máy A làm việc không quá 12 giờ một ngày nên ta có bất phương trình :

6x + 2y ≤ 12, hay 3x + y ≤ 6.

Để sản xuất x tấn sản phẩm X cần dùng máy B trong 2x (giờ) ; để sản xuất y tấn sản phẩm Y cần dùng máy B trong 2y (giờ).

Tổng số giờ dùng máy B trong một ngày là 2x + 2y (giờ).

Do máy B làm việc không quá 8 giờ một ngày nên ta có bất phương trình: 2x + 2y ≤ 8, hay x + y  ≤ 4.

Vậy ta có hệ bất phương trình:

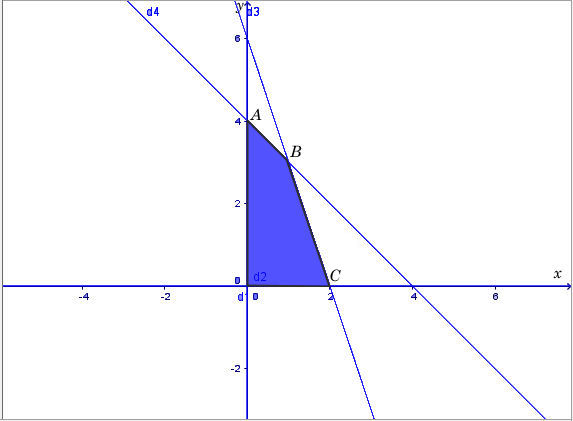
Miền nghiệm của hệ là miền tứ giác OABC (bao gồm cả các cạnh) với các đỉnh O(0; 0) ; A(0; 4); B(1; 3) ; C (2; 0)  .

Gọi F (triệu đồng) là số tiền lãi thu được.

Với x tấn sản phẩm X thì số tiền lãi là 10x (triệu đồng); với y tấn sản phẩm  Y thì số tiền lãi là 8y (triệu đồng). Tổng số tiền lãi là 10x + 8y (triệu đồng).

Do đó F =10x + 8y

Tính giá trị của F tại các đỉnh của tứ giác OABC :

Tại O(0; 0): F = 10.0 + 8.0 = 0;

Tại A(0; 4): F = 10.0 + 8.4 = 32.

Tại B(1; 3): F = 10.1 + 8.3 = 34;

Tại C(2; 0): F= 10.2 + 8.0 = 20;

F đạt giá trị lớn nhất là 34 tại B(1; 3) 

Vậy để tổng số tiền lãi cao nhất thì xưởng phải sản xuất 1 tấn sản phẩm X và 3 tấn sản phẩm Y.