Giải 1.29 Toán 12 tập 1 SGK Kết nối tri thức: Hàm số và giới hạn

Đề bài

Giả sử hàm cầu đối với một loại hàng hóa được cho bởi công thức:

Trong đó p là giá bán (nghìn đồng) của mỗi đơn vị sản phẩm và x là số lượng đơn vị sản phẩm đã bán.

a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.

b) Khảo sát sự biến thiên và vẽ đồ thị của hàm số x = x(p). Từ đồ thị đã vẽ, hãy cho biết:

- Số lượng đơn vị sản phẩm bán được sẽ thay đổi thế nào khi giá bán p tăng;

- Ý nghĩa thực tiễn của giới hạn 

Phân tích và Hướng dẫn giải

Bài toán yêu cầu chúng ta phân tích mối quan hệ giữa giá bán $p$ và số lượng sản phẩm bán ra $x$.

• Câu a: Chúng ta sẽ biến đổi công thức $p=p(x)$ thành công thức ngược $x=x(p)$. Sau đó, ta thay giá trị $p$ vào để tính $x$.

• Câu b: Dựa vào công thức $x=x(p)$ vừa tìm được, ta khảo sát sự biến thiên của hàm số này bằng cách tính đạo hàm và xét dấu. Đồng thời, ta tính giới hạn của hàm số khi $p$ tiến đến 0 từ phía dương để tìm ý nghĩa thực tiễn của nó.

Lời giải chi tiết bài 1.29 Toán 12

a) Tìm công thức tính x như là hàm số của p. Tìm tập xác định của hàm số này. Tính số đơn vị sản phẩm đã bán khi giá bán của mỗi đơn vị sản phẩm là 240 nghìn đồng.

Ta có: 

Tập xác định của hàm số là: (0; 354]

Với p = 240, ta có: 

Vậy với giá bán mỗi đơn vị sản phẩm là 240 nghìn đồng thì bán được 47,5 đơn vị sản phẩm.

b) Khảo sát sự biến thiên của hàm số:

 với mọi p ∈ (0; 354]

Hàm số không có cực trị.

Giới hạn: 

Nên p = 0 là tiệm cận đứng

Bảng biến thiên:

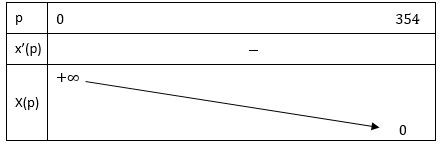
3. Đồ thị

Ta có: x(p) = 0 ⇔ p = 354

Đò thị hàm số x(p) cắt trục hoành tại điểm (354; 0); đi qua các điểm (300; 18); (200; 77)

Đồ thị x(p) với p ∈ (0; 354] là phần đường màu tím như hình sau:

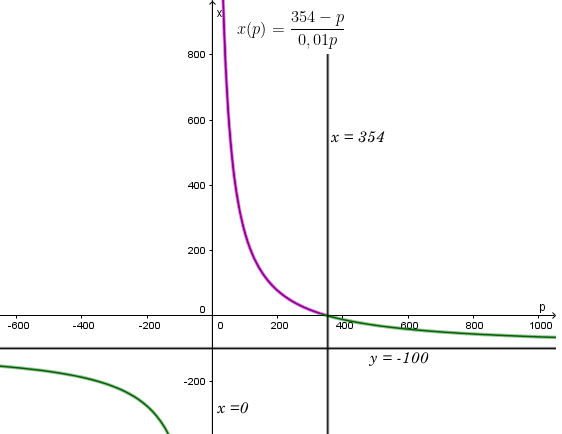
- Số lượng đơn vị sản phẩm bán sẽ giảm đi khi giá bán tăng, và sẽ không bán được sản phẩm nào nếu giá bán là 354 nghìn đồng

- Ý nghĩa thực tiễn của giới hạn : Vì nên giá bán càng thấp thì số lượng đơn vị sản phẩm sẽ bán được càng nhiều.