Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức

Bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức:

Cho hình chóp S.ABCD có đáy là hình chữ nhật và SA ⊥ (ABCD). Gọi M, N tương ứng là hình chiếu của A trên SB, SD. Chứng minh rằng:

AM ⊥ (SBC), AN ⊥ (SCD), SC ⊥ (AMN).

Giải bài 7.7 trang 36 Toán 11 tập 2 Kết nối tri thức:

* Cần nhớ: - Nếu một đường thẳng vuông góc với hai đường thẳng cắt nhau thuộc cùng một mặt phẳng thì nó vuông góc với mặt phẳng đó. Định nghĩa đường thẳng vuông góc mặt phẳng.

Ta có hình minh họa như sau:

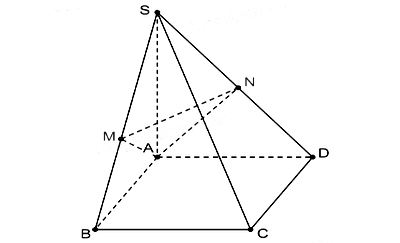
• Ta có: BC ⊥ AB (vì ABCD là HCN)

BC ⊥ SA ( vì SA ⊥ (ABCD))

AB ∩ SA = {A}

⇒ BC ⊥ (SAB) mà AM ⊂ (SAB)

⇒ BC ⊥ AM

• Ta có: CD ⊥ AD (vì ABCD là HCN)

 CD ⊥ SA ( vì SA ⊥ (ABCD))

AD ∩ SA = {A}

⇒ CD ⊥ (SAD) mà AN ⊂ (SAB)

⇒ CD ⊥ AN

• Ta có: AM ⊥ SB

 AM ⊥ BC

 SB ∩ BC = {B}

⇒ AM ⊥ (SBC); mà SC ⊂ (SBC)

⇒ SC ⊥ AM

• Ta có: AN ⊥ SD

 AN ⊥ CD

 SD ∩ CD = {D}

⇒ AN ⊥ (SCD); mà SC ⊂ (SCD)

⇒ SC ⊥ AN

• Ta có: AM ⊥ SC

 AN ⊥ SC

 AM ∩ AN = {A}

⇒ SC ⊥ (AMN)