Bài 5 trang 14 Toán 9 tập 1 Chân trời sáng tạo SGK

Đề Bài 5 trang 14 Toán 9 tập 1:

Cho hai đường thẳng   và y = –2x – 1

a) Vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ

b) Xác định tọa độ giao điểm A của hai đường thẳng trên

c) Tọa độ của điểm A có là nghiệm của hệ phương trình  không? Tại sao?

Phân tích và Hướng dẫn giải

Để giải quyết bài toán này, các em cần thực hiện các bước sau:

• Câu a: Vẽ đồ thị hai đường thẳng.

  • Với mỗi đường thẳng, các em cần tìm ít nhất hai điểm thuộc nó. Cách đơn giản nhất là cho $x=0$ để tìm giao điểm với trục Oy, và cho $y=0$ để tìm giao điểm với trục Ox.

  • Sau khi có hai điểm, các em nối chúng lại để vẽ đường thẳng.

• Câu b: Tìm tọa độ giao điểm A.

  • Dựa vào hình vẽ ở câu a, các em xác định tọa độ của điểm giao nhau của hai đường thẳng.

• Câu c: Kiểm tra mối quan hệ giữa giao điểm và nghiệm của hệ phương trình.

  • Các em cần biến đổi các phương trình trong hệ về dạng $y=ax+b$ để xem chúng có trùng với hai đường thẳng đã cho hay không.

  • Sau đó, thay tọa độ của điểm A tìm được ở câu b vào hệ phương trình để kiểm tra. Nếu cả hai phương trình đều thỏa mãn thì tọa độ A là nghiệm của hệ.

Lời giải chi tiết:

a) Vẽ hai đường thẳng đó trên cùng một hệ trục tọa độ

Với đường thẳng  ta xác định hai điểm A(0; 2) và B(4; 0)

Vẽ đường thẳng đi qua AB ta được đường  

Với y = –2x – 1 ta xác định hai điểm C(0; –1) và D(–1/2; 0)

Vẽ đường thẳng đi qua CD ta được đường y = –2x – 1

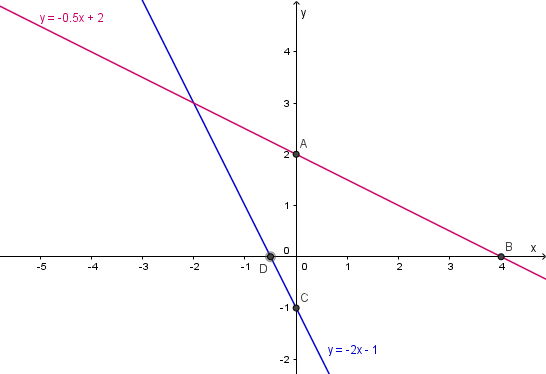
b) Xác định tọa độ giao điểm A của hai đường thẳng

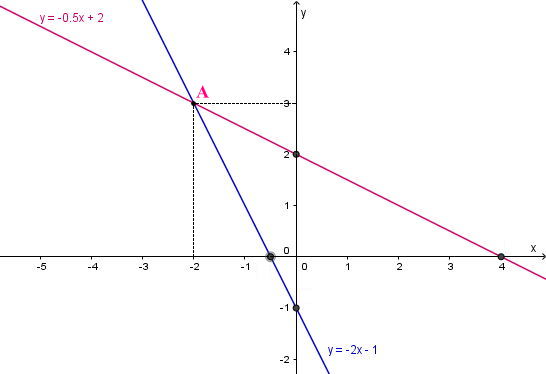
Từ hình vẽ, ta có thể xác định tọa độ giao điểm A(–2; 3).

c) Tọa độ của điểm A(–2; 3) là nghiệm của hệ phương trình  vì

Thay tọa độ A, x = –2 và y = 3 vào pt thứ nhất: –2 + 2.3 = 4 là nghiệm của pt thứ nhất

Thay tọa độ A, x = –2 và y = 3 vào pt thứ hai: 2.(–2) + 3 = –1 là nghiệm của pt thứ hai

Vậy tọa độ của điểm A(–2; 3) là nghiệm của hệ phương trình