Bài 3 trang 14 Toán 9 tập 1 Chân trời sáng tạo SGK

Đề Bài 3 trang 14 Toán 9 tập 1:

Hãy biểu diễn tất cả các nghiệm của mỗi phương trình sau trên mặt phẳng Oxy

a) 2x + y = 3

b) 0x – y = 3

c) –3x + 0y = 2

d) –2x + y = 0

Phân tích và Hướng dẫn giải

Tập hợp nghiệm của phương trình bậc nhất hai ẩn có dạng $ax+by=c$ luôn được biểu diễn bằng một đường thẳng trên mặt phẳng tọa độ Oxy. Để biểu diễn đường thẳng này, các em cần làm theo các bước sau:

• Bước 1: Biến đổi phương trình

  • Đối với các phương trình có cả $x$ và $y$ (như câu a và d), hãy biến đổi để có dạng $y=mx+n$.

  • Đối với các phương trình chỉ có một ẩn (như câu b và c), hãy biến đổi để có dạng $y=k$ hoặc $x=h$.

• Bước 2: Tìm hai điểm bất kỳ thuộc đường thẳng

  • Chọn một giá trị bất kỳ cho $x$ (hoặc $y$), sau đó tính giá trị tương ứng của ẩn còn lại.

  • Lặp lại bước trên để tìm một cặp điểm khác.

• Bước 3: Biểu diễn trên mặt phẳng Oxy

  • Đặt hệ trục tọa độ Oxy.

  • Xác định vị trí của hai điểm vừa tìm được.

  • Vẽ đường thẳng đi qua hai điểm đó.

Lời giải chi tiết:

a) 2x + y = 3

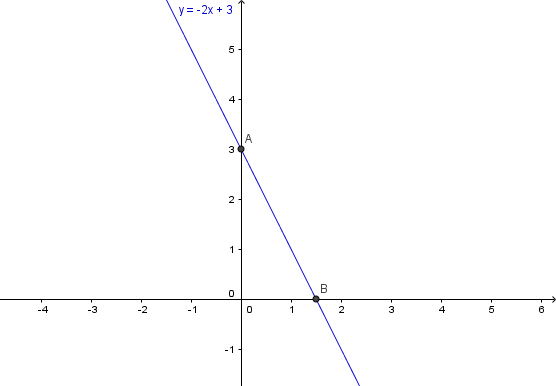
Viết lại phương trình thành y = –2x + 3

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = –2x + 3, như sau:

b) 0x – y = 3

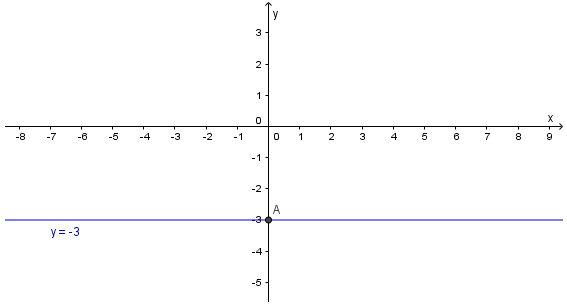
Viết lại phương trình thành y = –3

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = –3, như sau:

c) –3x + 0y = 2

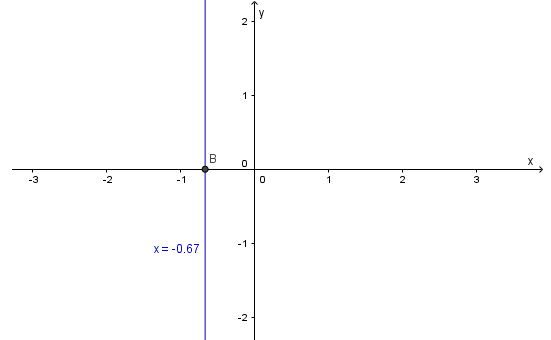
Viết lại phương trình thành x = –2/3

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: x = –2/3, như sau:

d) –2x + y = 0

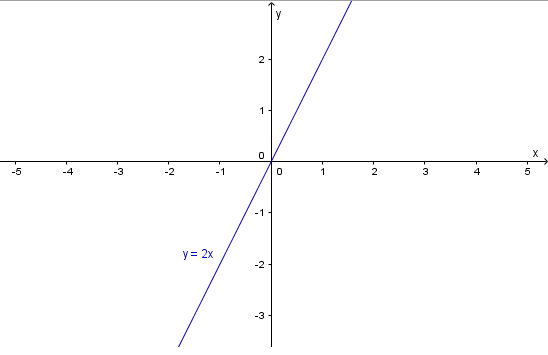
Viết lại phương trình thành y = 2x

Từ đó, tất cả các nghiệm của phương trình đã cho được biểu diễn bởi đường thẳng d: y = 2x, như sau: