Hotline 0936685849

Bài 1.24 trang 32 Toán 12 tập 1 Kết nối tri thức

09:36:5922/03/2024

Chào các em! Bài viết này sẽ hướng dẫn các em giải chi tiết Bài 1.24 trang 32 SGK Toán 12 thuộc bộ sách Kết nối tri thức với cuộc sống tập 1. Đây là một bài toán ứng dụng thực tế về nồng độ dung dịch, giúp các em vận dụng kiến thức về hàm số, giới hạn và đồ thị để giải quyết.

Đề bài:

Một cốc chứa 30ml dung dịch KOH (potassium hydroxide) với nồng độ 100mg/ml. Một bình chứa dung dịch KOH khác chứa nồng độ 8mg/ml được trộn vào cốc.

a) Tính nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa, kí hiệu là C(x).

b) Coi hàm C(x) là hàm số xác định với x ≥ 0. Khảo sát sự biến thiên và vẽ đồ thị của hàm số này.

c) Giải thích tại sao nồng độ KOH trong cốc giảm theo x nhưng luôn lớn hơn 8mg/ml.

Phân tích và Hướng dẫn giải:

Bài toán cho biết một cốc chứa dung dịch KOH nồng độ 100 mg/ml và một bình khác chứa dung dịch KOH nồng độ 8 mg/ml. Cần giải quyết ba yêu cầu:

a) Lập hàm số nồng độ $C (x)$ : Biểu thức nồng độ sẽ được tính bằng cách lấy tổng khối lượng chất tan chia cho tổng thể tích dung dịch.

b) Khảo sát và vẽ đồ thị hàm số: Sau khi có hàm số $C (x)$ , ta sẽ khảo sát sự biến thiên của nó trên miền xác định $x \geq 0$ và vẽ đồ thị.

c) Giải thích ý nghĩa của đồ thị: Dựa vào tính chất của hàm số (đồng biến/nghịch biến) và giới hạn của nó, ta sẽ giải thích ý nghĩa của nồng độ dung dịch.

Lời giải chi tiết:

a) Khối lượng dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là:

m = 30.100 + 8x = 8x + 3000 (mg)

Thể tích dung dịch trong cốc sau khi trộn x(ml) KOH từ bình chứa là:

V = 30 + x (ml)

Nồng độ KOH trong cốc sau khi trộn x (ml) từ bình chứa là:

$C(x)=\frac{m}{V}=\frac{8x+3000}{30+x}(mg/ml)$

b) Khảo sát hàm số $y= C(x)=\frac{8x+3000}{30+x}(mg/ml)$

• TXĐ: D = [0; +∞)

• Sự biến thiên:

$C'(x)=\frac{-2760}{(x+30)^2}<0$ với mọi x ∈ D

Hàm số nghịch biến trên (0; +∞)

Hàm số không có cực trị

$\lim_{x\rightarrow +\infty }y=\lim_{x\rightarrow +\infty }\frac{8x+3000}{x+30}=8$

Nên y = 8 là tiệm cận ngang của đồ thị hàm số

• Bảng biến thiên:

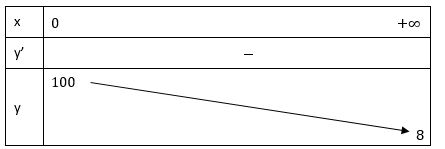
BBT bài 1.24 trang 32 Toán 12 Tập 1 Kết nối tri thức

• Đồ thị:

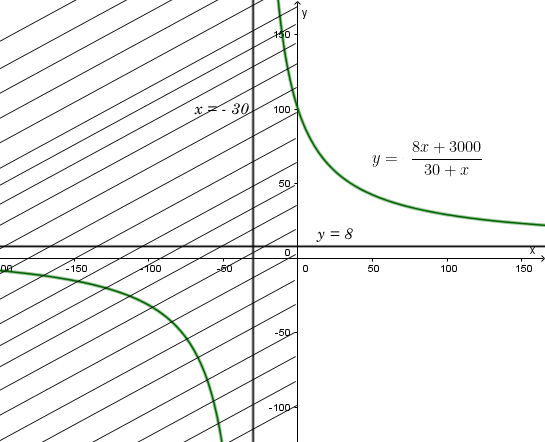
Đồ thị bài 1.24 trang 32 Toán 12 Tập 1 Kết nối tri thức

Đồ thị hàm số là phần không bị gạch chéo.

c) Vì $C'(x)=\frac{-2760}{(x+30)^2}<0$ với mọi x ∈ D

và $\lim_{x\rightarrow +\infty }C(x)=\lim_{x\rightarrow +\infty }\frac{8x+3000}{x+30}=8$

Hàm số nghịch biến: Vì $C^{'} (x) < 0$ với mọi $x \geq 0$ , nên nồng độ $C (x)$ là hàm giảm. Điều này có nghĩa là khi ta thêm dung dịch KOH có nồng độ thấp hơn (8 mg/ml) vào cốc có nồng độ cao hơn (100 mg/ml), nồng độ trung bình của cốc sẽ giảm dần.

Giới hạn tiệm cận: Giới hạn của $C (x)$ khi $x \to + \infty$ là 8. Điều này có nghĩa là nếu ta thêm một lượng rất lớn dung dịch có nồng độ 8 mg/ml, nồng độ trong cốc sẽ dần tiến đến 8 mg/ml nhưng không bao giờ đạt được giá trị đó. Do đó, nồng độ KOH trong cốc luôn lớn hơn 8 mg/ml.