Bài 1.22 trang 32 Toán 12 tập 1 Kết nối tri thức

Dề bài:

Khảo sát sự biến thiên và vẽ đồ thị của các hàm số sau:

a) 

b) 

Phân tích và Hướng dẫn giải:

Để khảo sát sự biến thiên và vẽ đồ thị của hàm số , ta thực hiện các bước sau:

1. Tìm tập xác định (TXĐ) của hàm số.

2. Xét sự biến thiên:

   • Tính đạo hàm y'.

   • Nhận xét dấu của y' để tìm các khoảng đồng biến và nghịch biến.

   • Tìm các đường tiệm cận đứng và tiệm cận ngang bằng cách xét giới hạn.

   • Lập bảng biến thiên.

3. Vẽ đồ thị:

   • Tìm các giao điểm của đồ thị với các trục tọa độ.

   • Vẽ các đường tiệm cận và các giao điểm.

   • Dựa vào bảng biến thiên để vẽ đồ thị một cách chính xác.

Lời giải chi tiết:

a) 

• Tập xác định: D = R\{-1}

• Sự biến thiên:

 với mọi x ∈ D.

Hàm số đồng biến trên khoảng (-∞; -1) và (-1; +∞)

• Hàm số không có cực trị.

• Tiệm cận:

Nên y = 2 là tiệm cận ngang của hàm số

Nên x = -1 là tiệm cận đứng của hàm số

• Bảng biến thiên:

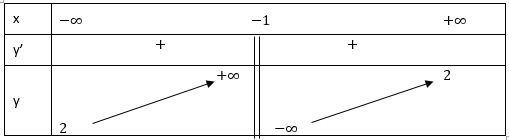
• Đồ thị

y = 0 ⇔ x = -1/2 giao điểm của đồ thị hàm số với trục hoành là điểm (-1/2; 0)

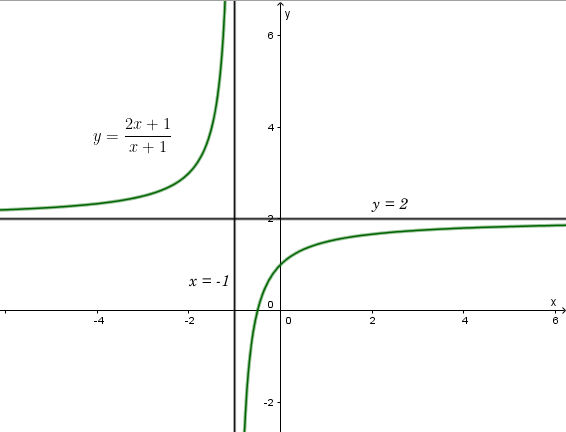
Đồ thị hàm số nhận giao điểm I(-1; 2) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.

b) 

• Tập xác định: D = R\{1}

• Sự biến thiên:

  với mọi x ∈ D.

Hàm số đồng biến trên khoảng (-∞; 1) và (1; +∞)

• Hàm số không có cực trị.

• Tiệm cận:

Nên y = -1 là tiệm cận ngang của hàm số

Nên x = 1 là tiệm cận đứng của hàm số

• Bảng biến thiên:

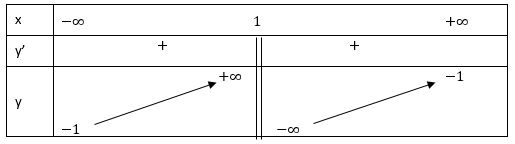
• Đồ thị

y = 0 ⇔ x = -3 giao điểm của đồ thị hàm số với trục hoành là điểm (-3; 0)

x = 0 ⇔ y = 3 giao điểm của đồ thị hàm số với trục tung là (0; 3).

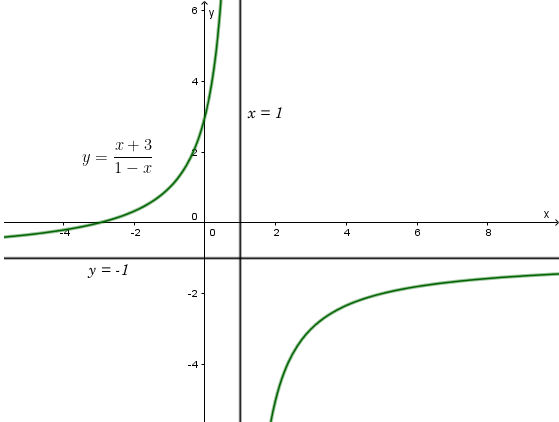
Đồ thị hàm số nhận giao điểm I(1; -1) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của góc tạo bởi hai đường tiệm cận này làm các trục đối xứng.