Giải bài 9 trang 61 Toán 10 Tập 1 SGK Cánh Diều

Đề bài:

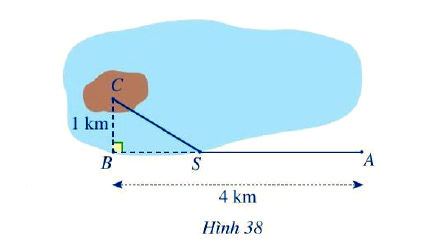
Một kĩ sư thiết kế đường dây điện từ vị trí A đến vị trí S và từ vị trí S đến vị trí C trên cù lao như Hình 38. Tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S và từ S đến C lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.

Phân tích và Hướng dẫn giải:

Bài toán yêu cầu tính tổng số ki-lô-mét đường dây điện đã thiết kế. Để giải, chúng ta sẽ thực hiện các bước sau:

1. Đặt ẩn và tìm mối liên hệ: Đặt số ki-lô-mét đường dây từ $A$ đến $S$ là $x$. Dựa vào hình vẽ và định lý Pythagore, biểu diễn độ dài đường dây từ $S$ đến $C$ theo $x$.

2. Lập phương trình: Sử dụng thông tin về tiền công để lập phương trình biểu thị tổng số tiền công.

3. Giải phương trình: Giải phương trình chứa căn vừa lập để tìm giá trị của $x$.

4. Tính tổng quãng đường: Tính tổng độ dài đường dây từ $A$ đến $S$ và từ $S$ đến $C$ để tìm tổng số ki-lô-mét đã thiết kế.

Lời giải chi tiết:

Gọi số ki-lô-mét đường dây điện từ vị trí A đến vị trí S là x (km) (x > 0). 

Khi đó trên hình vẽ ta có: SA = x km, AB = 4 km, BC = 1 km. 

Ta thấy AB = SA + SB, suy ra SB = AB – SA = 4 – x (km). (do SB > 0 nên 4 – x > 0 hay x < 4)

Lại có tam giác SBC vuông tại B nên theo định lý Pythagore ta có: 

SC² = BC² + BS² = 1² + (4 – x)² 

= 1 + 16 – 8x + x² = x² – 8x + 17

Vì tiền công thiết kế mỗi ki-lô-mét đường dây từ A đến S là 3 triệu đồng nên số tiền để thiết kế toàn bộ đường dây từ A đến S là: 3x (triệu đồng).

Tiền công thiết kế mỗi ki-lô-mét đường dây từ S đến C là 5 triệu đồng nên số tiền để thiết kế toàn bộ đường dây từ S đến C là:

 (triệu đồng)

Tổng số tiền công thiết kế toàn bộ đường dây từ A đến S và từ S đến C là 16 triệu đồng nên ta có phương trình:

Ta cần giải phương trình:  (*)

Trước hết ta giải bất phương trình: 16 – 3x > 0 ⇔ x < 16/3.

Mà 0 < x < 4 nên điều kiện của phương trình (*) là 0 < x < 4. 

Bình phương hai vế của (*) ta được: 25.(x² – 8x + 17) = (16 – 3x)²

⇔ 25x² – 200x + 425 = 256 – 96x + 9x²

⇔ 16x² – 104x + 169 = 0

⇔ x = 3,25 (thỏa mãn điều kiện). 

Vì vậy, số ki-lô-mét đường dây từ vị trí A đến S là 3,25 km

Số ki-lô-mét đường dây từ vị trí S đến C là:

Vậy tổng số ki-lô-mét đường dây đã thiết kế là: 3,25 + 1,25 = 4,5 (km).