Giải bài 4.7 trang 83 Toán 8 Tập 1 SGK Kết nối tri thức

Bài 4.7 trang 83 Toán 8 Tập 1 Kết nối tri thức:

Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC.

a) Chứng minh tứ giác BMNC là hình thang.

b) Tứ giác MNPB là hình gì? Tại sao?

Giải bài 4.7 trang 83 Toán 8 Tập 1 Kết nối tri thức:

Ta có hình minh hoạ như sau:

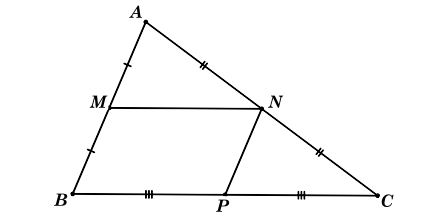
a) Vì M, N lần lượt là trung điểm của các cạnh AB, AC nên MN là đường trung bình của ΔABC

⇒ MN // BC.

Vậy tứ giác BMNC có MN // BC nên tứ giác BMNC là hình thang (đpcm).

b) Vì N, P lần lượt là trung điểm của các cạnh AC, BC nên NP là đường trung bình của ΔABC

⇒ NP // AB hay NP // MB.

Tứ giác MNPB có MN // BP (do MN // BC); BM // NP (chứng minh trên).

⇒ Tứ giác MNPB là hình bình hành.