Giải bài 4.17 trang 88 Toán 8 Tập 1 SGK Kết nối tri thức

Bài 4.17 trang 88 Toán 8 Tập 1 Kết nối tri thức:

Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM² = MN.MK.

Giải bài 4.17 trang 88 Toán 8 Tập 1 Kết nối tri thức:

Ta có hình minh hoạ như sau:

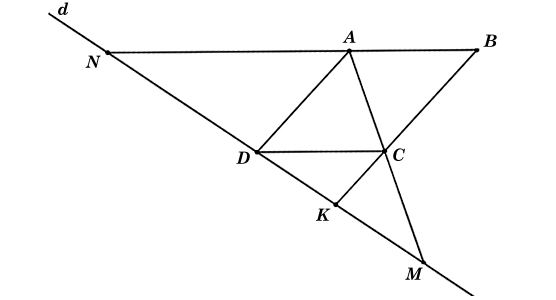
Vì ABCD là hình bình hành nên AB // CD, AD // BC

⇒ AN // CD và AD // CK.

Áp dụng định lí Thalès vào ΔAMN có AN // CD, ta được:

  (*)

Áp dụng định lí Thalès vào ΔADM có CK // AD, ta được:

  (**)

Từ (*) và (**) ta có:

⇒ DM² = MN.MK (đpcm).