Giải bài 4.15 trang 88 Toán 8 Tập 1 SGK Kết nối tri thức

Bài 4.15 trang 88 Toán 8 Tập 1 Kết nối tri thức:

Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E. Chứng minh rằng 

Giải bài 4.15 trang 88 Toán 8 Tập 1 Kết nối tri thức:

Ta có hình minh hoạ như sau:

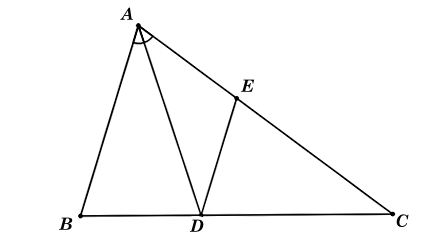
Theo đề bài, AD là tia phân giác của ,

Áp dụng tính chất đường phân giác vào ΔABC, ta có:  (*)

Đường thẳng qua D song song với AB cắt AC tại E hay DE // AB,

Áp dụng định lí Thalès vào ΔABC, ta có: 

  (**)

Từ (*) và (**) suy ra:  (đpcm)