Hotline 0936685849

Giải bài 4.16 trang 88 Toán 8 Tập 1 SGK Kết nối tri thức

10:24:2530/09/2023

Hôm nay chúng ta sẽ cùng nhau giải chi tiết Bài 4.16 trang 88 sách giáo khoa Toán 8 Tập 1, bộ sách Kết nối tri thức với cuộc sống. Bài toán này giúp các em ôn tập về tính chất đường phân giác và cách tính tỉ số diện tích của hai tam giác.

Đề bài:

Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.

a) Tính độ dài các đoạn thẳng DB và DC.

b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

Phân tích và Hướng dẫn giải:

Để giải quyết bài toán này, chúng ta sẽ thực hiện các bước sau:

Tính độ dài các đoạn thẳng DB và DC:
- Áp dụng tính chất đường phân giác trong tam giác. Cụ thể, đường phân giác của một góc trong tam giác chia cạnh đối diện thành hai đoạn thẳng tỉ lệ với hai cạnh kề hai đoạn thẳng đó.
- Sử dụng tính chất của dãy tỉ số bằng nhau để tìm độ dài của $D B$ và $D C$ .
Tính tỉ số diện tích của hai tam giác ABD và ACD:
- Ta nhận thấy hai tam giác này có chung đường cao hạ từ đỉnh $A$ xuống cạnh $BC$ .
- Tỉ số diện tích của hai tam giác có chung đường cao bằng tỉ số độ dài hai cạnh đáy tương ứng.

Lời giải chi tiết:

a) Tính độ dài các đoạn thẳng DB và DC.

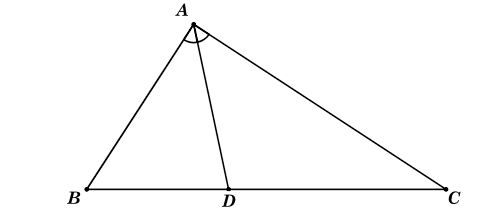
giải câu a bài 4.16 trang 88 Toán 8 Tập 1 Kết nối tri thức

Áp dụng tính chất đường phân giác, ta có:

$\small \frac{DB}{DC}=\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}$

$\small \Rightarrow \frac{DB}{3}=\frac{DC}{4}$

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\small \frac{DB}{3}=\frac{DC}{4}=\frac{DB+DC}{3+4}$ $\small =\frac{BC}{7}=\frac{25}{7}$

$\small \Rightarrow DB=\frac{3.25}{7}=\frac{75}{7}(cm)$

$\small \Rightarrow DC=\frac{4.25}{7}=\frac{100}{7}(cm)$

Vậy: $\small DB=\frac{75}{7}(cm);\: DC=\frac{100}{7}(cm)$

b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

Hai ΔABD và ΔACD có chung đường cao kẻ từ đỉnh A đến cạnh BC, ta gọi đường cao đó là AH.

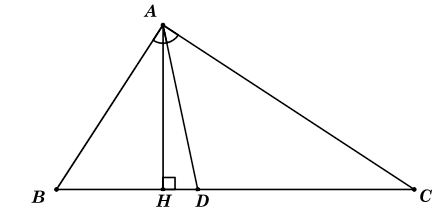Giải câu b bài 4.16 trang 88 Toán 8 Tập 1 Kết nối tri thức Ta có:

$\small S_{\Delta ABD}=\frac{1}{2}AH.DB$

$\small S_{\Delta ADC}=\frac{1}{2}AH.DC$

Suy ra:

$\small \frac{S_{\Delta ABD}}{S_{\Delta ADC}}=\frac{\frac{1}{2}AH.DB}{\frac{1}{2}AH.DC}=\frac{DB}{DC}=\frac{3}{4}$

Vậy tỉ số diện tích của hai tam giác ABD và ACD bằng 3/4.

Qua bài tập này, các em đã ôn lại hai kiến thức quan trọng: tính chất đường phân giác giúp xác định tỉ lệ độ dài các đoạn thẳng, và mối quan hệ giữa tỉ số diện tích với tỉ số độ dài đáy của hai tam giác có chung đường cao. Việc nắm vững hai khái niệm này là rất hữu ích để giải quyết các bài toán hình học phức tạp hơn.

• Xem thêm:

Bài 4.13 trang 88 Toán 8 Tập 1 Kết nối tri thức: Tìm độ dài x trong Hình 4.30...

Bài 4.14 trang 88 Toán 8 Tập 1 Kết nối tri thức: Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC...

Bài 4.15 trang 88 Toán 8 Tập 1 Kết nối tri thức: Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E...

Bài 4.17 trang 88 Toán 8 Tập 1 Kết nối tri thức: Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K...